今回は、2次元の有限要素法における面積座標(局所座標)の積分公式 を示します。ここで は2次元の三角形要素、 はその面積、、、 は形状関数で、それぞれ とあらわされます。係数は で与えられます。 と はそれぞれ三角形要素の頂点の座標です。 これを知っていると積分がサクサクでき積分法(せきぶんほう、英 integral calculus )は、微分法と共に微分積分学で対を成す主要な分野である。 実数直線上の区間 a, b 上で定義される実変数 x の関数 f の定積分 (独 bestimmtes Integral, 英 definite integral, 仏 intégrale définie) ()は、略式的に言えば f のグラフと x軸、および x = a と r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。
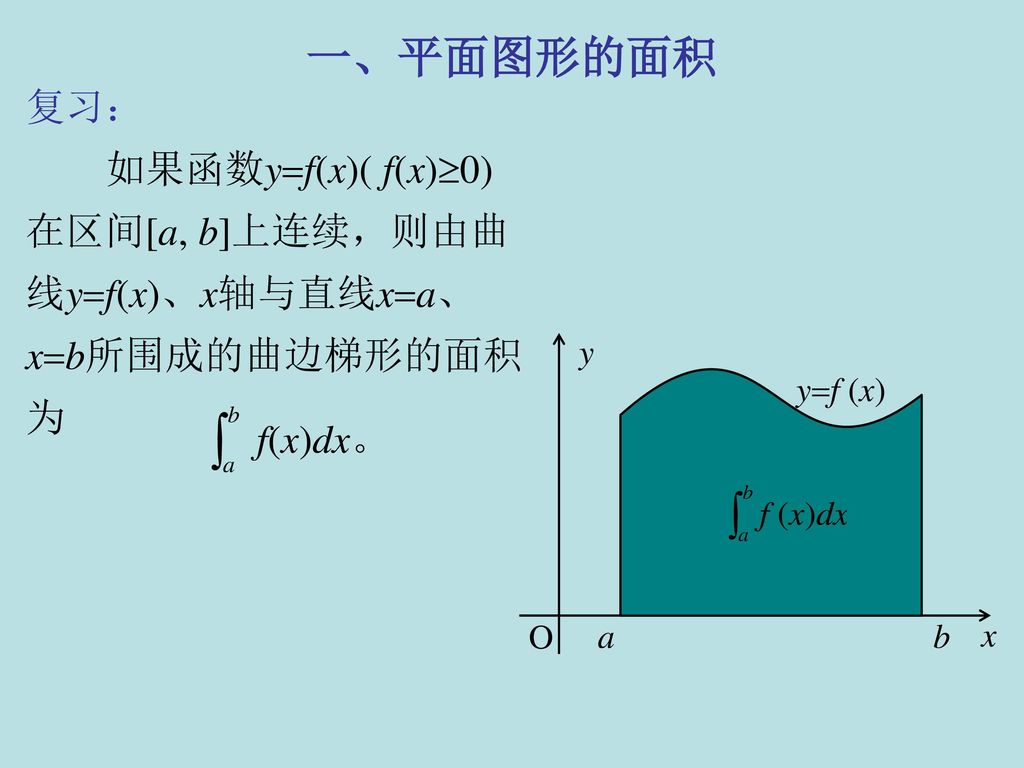
第十章定积分的应用 一 一 平面图形的面积面积公式 直角坐标 极坐标 二 由平行截面面积求体积由平行截面面积求体积
面積公式 積分
面積公式 積分-積分の公式 積分の公式は下記です。 A=∫dA 例えば∫に「下添え字0、上添え字10」という数値が付きました。微小面積dAは、0~10の範囲まで積分を行う、という意味です。 なぜ積分で面積を計算するのか? 積分を使って面積の求め方を説明しました。跟求面積一樣,我們可能想知道一個物體的體積。 因此我們可以利用黎曼積分來定義所謂的體積: 注意到,若當A(x) = A 為常數的話,則體積的積分為A(ba) 也就與原本我們所認識的柱體體積公式相符。



Ppt 第五章積分powerpoint Presentation Free Download Id
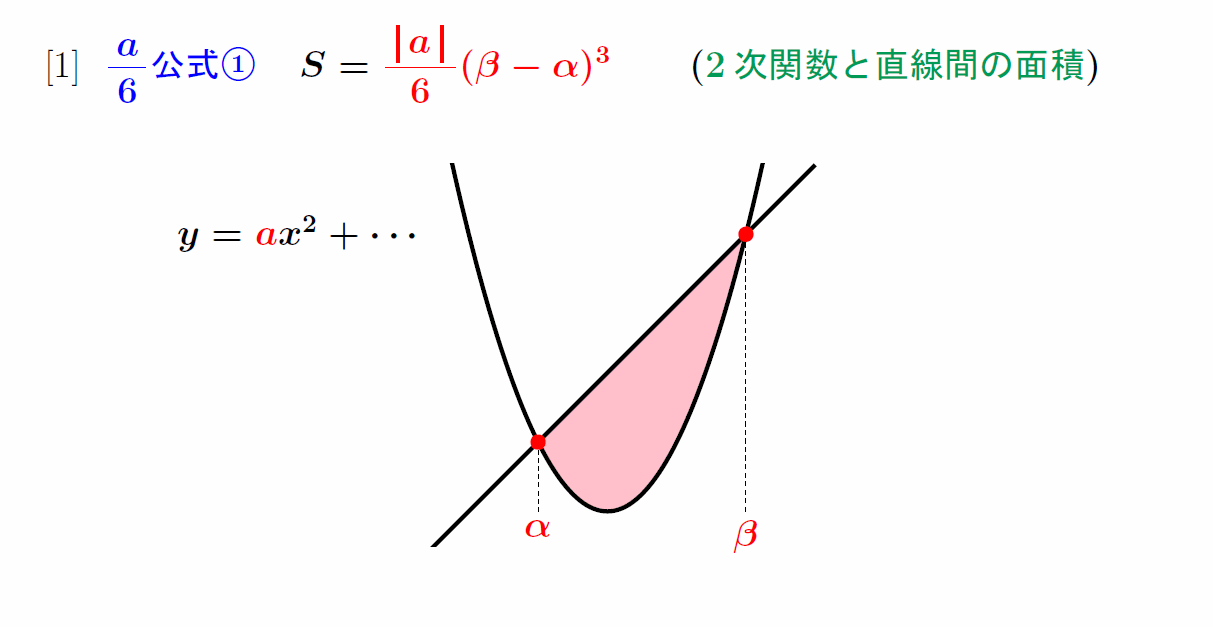
X 囲まれたグラフがどこの位置に あろうと常に上下で求めること ができる! S x=β x =β =β β x x =β =α α α β x y = ax2 qx r y = px2 qx r y = ax2 bx c y = ax2 bx c y = ax2 bx c y = ax2 bx c x =αβ 2 = (βα) a球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる如何在Excel中計算繪製曲線下的面積? 學習積分時,您可能已經繪製了一條繪製的曲線,在曲線下方陰影了一個區域,然後計算陰影部分的面積。 在這裡,本文將介紹兩種在Excel中計算繪製曲線下面積的解決方案。 您可以使用以下公式輕鬆計算其面積: =(C3C4
定積分とは、「任意の範囲の面積の値そのもの」のことです。 上の例では、関数 f (x) = 2x の 2,5 間の面積は、 F (5)−F (2) = 21 でした。 同じように 0,2 間の面積は、 F (2)− F (0) = 4 となります。 東大塾長の山田です。このページでは、「積分の面積公式」について解説します。積分で面積を求める有名な公式「1 / 6公式」,その他にも,曲線と接線の間の面積を求める「1 / 3公式」,「1 / 12公式」についても詳しく解説しているので,ぜひ勉強の参考にしてください!に公式として授業で触れることは避けた。 記号の導入などの説明が一通り終わったら,不定 積分,定積分の定義を定着させるために,不定積分, 定積分の計算演習を十分に行わせた。 34.積分の計算を活用して,関数のグラフで囲まれ た部分の面積を求める
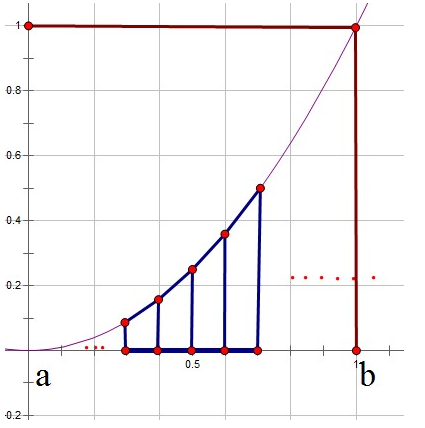
積分 面積 裏技公式を1枚にまとめた早見チャートです。 面積 裏技 裏ワザ 暗記 微分 極限 体積 チャート 参考書 2次関数 方程式 放物線 二次関数 2次関数 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックする(面積の復習) a≦x≦b の区間で x 軸と y=f(x) とで囲まれる図形の面積が,縦の長さ f(x) の積分で表された事情を振り返ってみます. a から x までに描かれる図形の面積を S(x) とおくと x がわずかに ⊿x だけ増加したとき,増える面積は黄色で示した長方形の面積,すなわち縦の長さ f(x) と横の定積分 這樣的極限 在我們討論f 函數曲線下的面積,或者討論給定速度的情況 下求位移的距離,都會考慮到這樣的極限。 我們還會遇到更多這樣的情況,在更一般的情況下,甚至f(x) 也不一定是正值的函數,但是我們也是有一樣的概念。




積分の面積公式と証明 6分の1公式 接線など 理系ラボ




第六章定积分的应用利用元素法解决 定积分在几何上的应用 L P184 定积分在物理上的应用 Ppt Download
積分の公式一覧 Tooda Yuuto 18年3月19日 / 年2月10日 積分の公式は、微分の公式をひっくり返して考えると覚えやすいです。 微分積分I 公式一覧 on Math 高専2年の数学の教科書として使用した「新 微分積分 I」(大日本図書) の公式などを備忘録としてまとめたものです。の図形の面積は Z Z ff(x;y)‚0g dxdy (f は(x;y) の滑らかな関数または区分的に滑らかな関数) と表すことが出来た。3 次元でも同じ様に空間を分割することによって積分を定 義するので、同様のことができる。 例131 球x 2 y z2 • a2 と円柱(x ¡ a 2)2 y2 • (a 2)2



积分计算两条曲线围绕y坐标轴旋转形成的立体体积 Zhang Phil Csdn博客 积分绕y轴旋转的体积公式




Python 计算离散点的微分和积分 超详细 Goodcodevsbadbs的博客 程序员宅基地 Python 离散点求导 程序员宅基地
面積の基本①(x軸方向への定積分) 面積の基本②(y軸方向への定積分) 接線と面積, 接する2曲線と面積; 広義積分の計算方法とその理解の仕方~そんな計算していいの? ? ~ 解析学A (1変数の微積分)や解析学B (多変数の微積分)では、「広義積分」と呼ばれる内容を学習することになります。 「広義」とありますが、これは「広い意味での」ということです 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p




定积分求圆的面积 圆面积积分 三人行教育网 Www 3rxing Org




定积分求面积步骤 百度经验
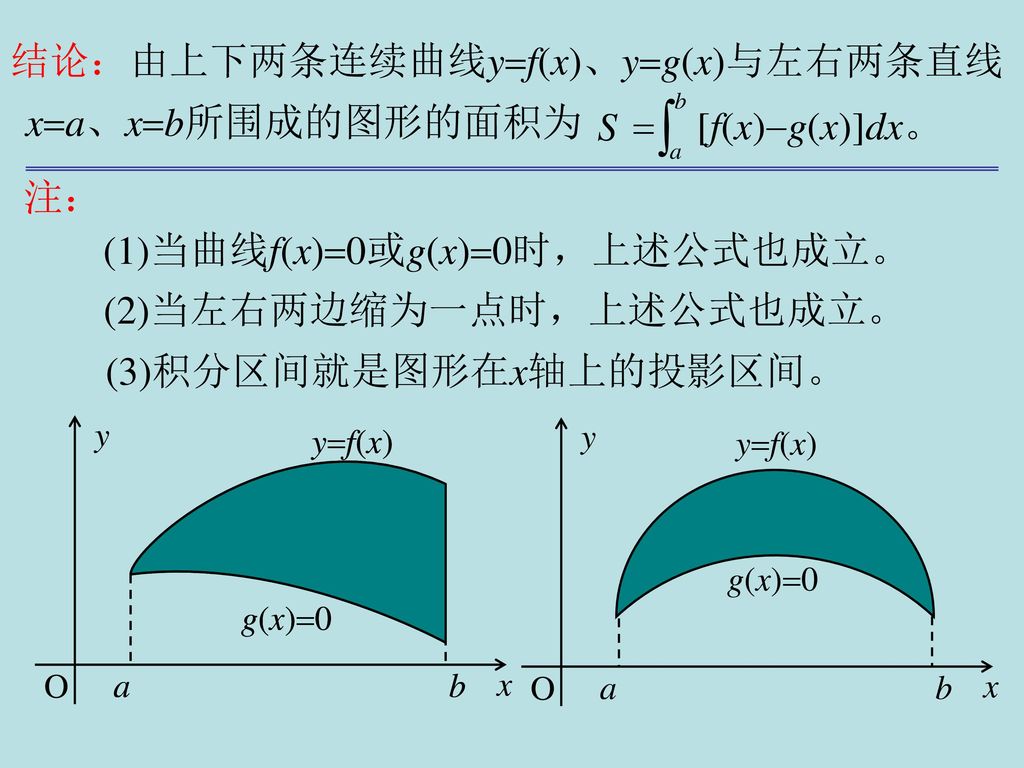
面積と定積分の関係について,次のことが成り立ちます。 関数 y = f(x) が a ≦ x ≦ b において連続であり, f(x) ≧ 0 を満たしているとき,2直線 x = a , x = b と x 軸, y = f(x) のグラフで囲まれた図形の面積は,定積分 ∫b af(x)dx の値に等しくなります。 x y = f 定積分とは?公式や面積の計算、絶対値を含む問題の解き方 さまざまな関数の積分公式 関数の種類に応じた積分公式が存在します。 不定積分の形で公式を示していますが、定積分でも成 単元 積分, 「積分分野で有名な面積の公式を色つきでまとめました センター試験が近づいてくるしこれを身につければ数2bの時間が一気に短縮ミスもしにくくて得点up!! 補足としてこの公式の元になった積分の公式をまとめました 注意としては、ここの公式は主にマーク式の試験で




圆的面积公式 圆的面积公式是怎么得到的 52fmz购物网




积分 维基百科 自由的百科全书
積分の微分 積分を微分したら元に戻るんじゃないの? そう思った人はその通りです。 微分の逆として考えたのが積分 でしたものね。 ですが今扱いたいのは 「定積分」の「微分」 です。 定積分は面積と関わりがありましたがこれを微分したら何が起こるのでしょうか。149 積の ここで,Δx →0 のとき, dS =2πy √ 1 +( dy) 2 となるので, この両辺を x で,区間a,b で積分することにより,この x 軸のま わりの回転体の曲面の表面積 S が,次式で求められるんだね。 (Ⅱ) についても同様に,微小区間y, y+Δにおける微小な曲面の表面積 ΔS は,数学 公式集 複素数 代数学式の計算 数学 公式集 積分 Integral 数学ハンドブック 数学-公式集 記号-単位 物理学ハンドブック 公式集 (面積・体積) 微分 導関数




Ppt 第五章積分powerpoint Presentation Free Download Id



Q Tbn And9gcrxrw7 Um5jpuzzqblohrmzui Zwisxv7jrpthk1fc4mcyvocgy Usqp Cau
1/6 (βα)^3 の積分の公式の説明のおわりに いかがでしたか? 関数によって囲まれた部分の面積を求める問題は頻出です。公式集:積分 基本となる関数の積分 : これだけは覚えておこう. 置換積分法 : 変数の置き換えによって積分の計算を簡単にする手法 部分積分法 : 関数の積 の積分の計算を簡単にする手法 知っていると便利な積分の公式 定積分の基本式 : 面積の計算,体積の計算,曲線の長さの計算 これらの公式の理解においては, 1 6 \dfrac{1}{6} 6 1 公式の証明で見たような「定積分における x − α x\alpha x − α を基準にする考え方」が重要です。




定积分面积公式 如何用定积分求面积总结一下用到的所有公式 包括极坐 三人行教育网 Www 3rxing Org



5 10 定积分的应用
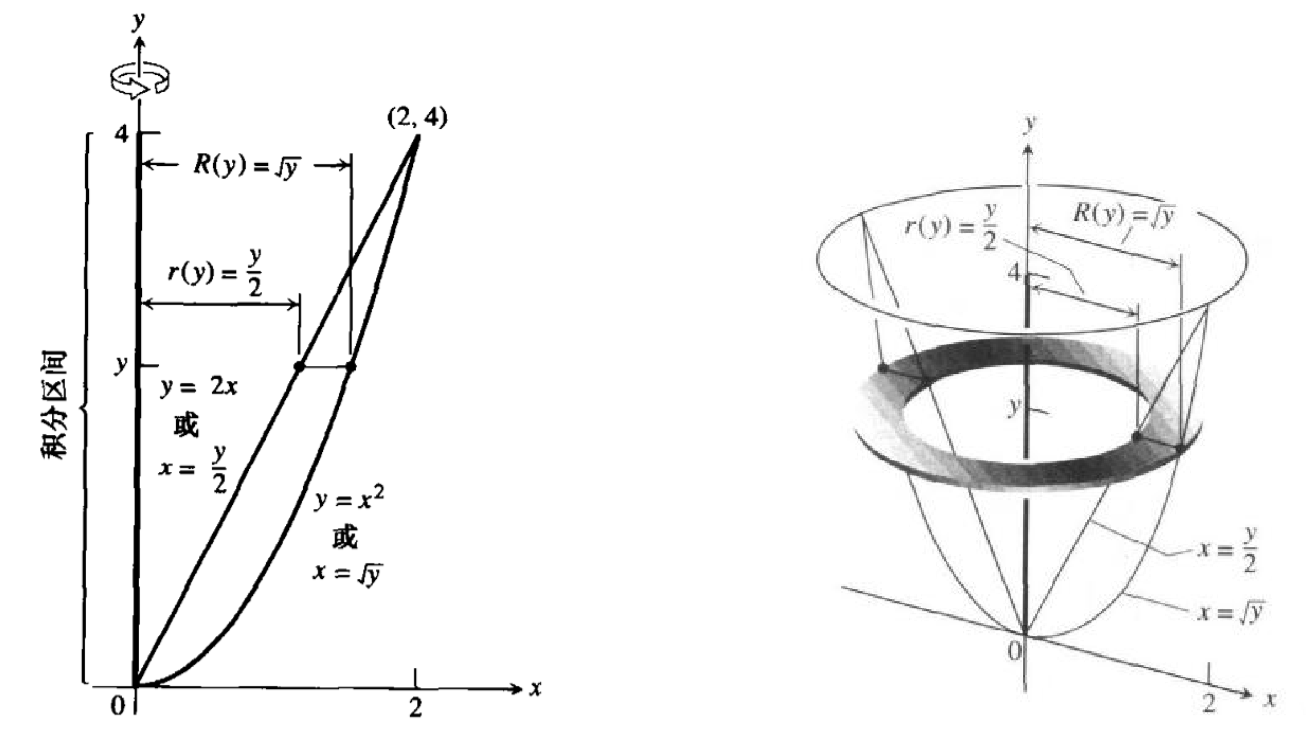
積分計算による体積の求め方! 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通して 媒介変数表示されたグラフの面積の求め方を例題付きで解説! 検算に使える定理も教えます! 1 媒介変数表示されたグラフの面積の求め方は? 11 パラメータで微分してグラフの概形を描く 12 積分の式を立てる 13 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい



文章 用定积分求面积的两个重要公式 1 5定积分 高中苏教版 数学中国网
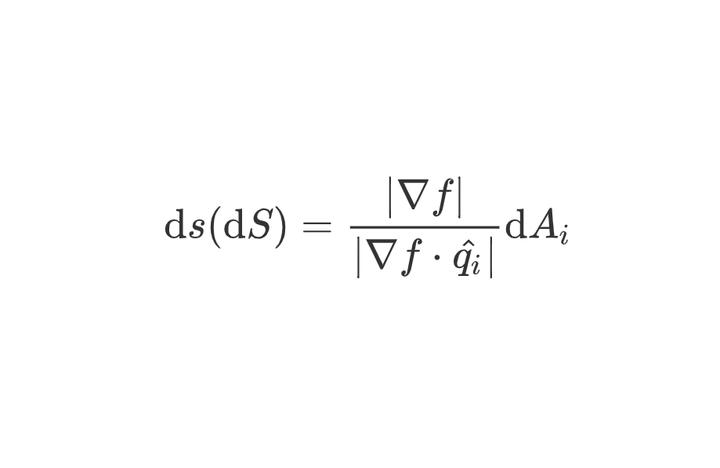



线积分与面积分 2 最初的公式 知乎
すると円の面積 S S は S = πR2 S = π R 2曲線x a +y b =1の面積とベータ関数




センター数学最強 A 6 A 12 A 3面積裏技公式 大学入試共通テスト 受験の月
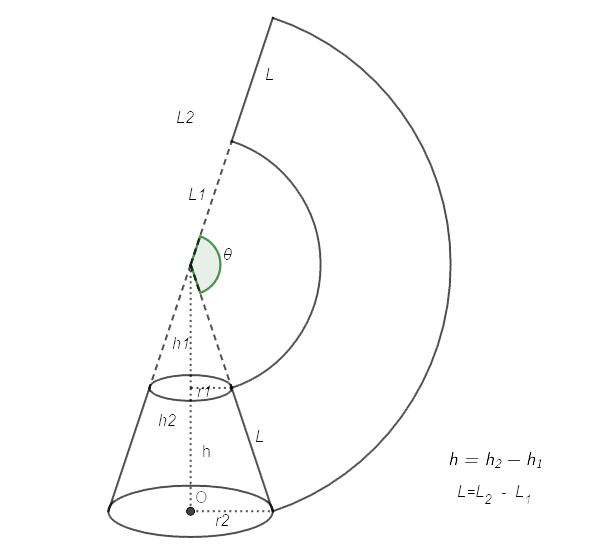



圆台侧面积和体积计算公式推导 冰雪 悦灵 博客园




用微积分来计算不规则图形的体积 人人焦点



積分単元 面積公式 時習館 ゼミナール 高等部




球面積計算球 Yxhsa




使用数学中的微积分推导出椭圆的的面积公式a Pab Youtube
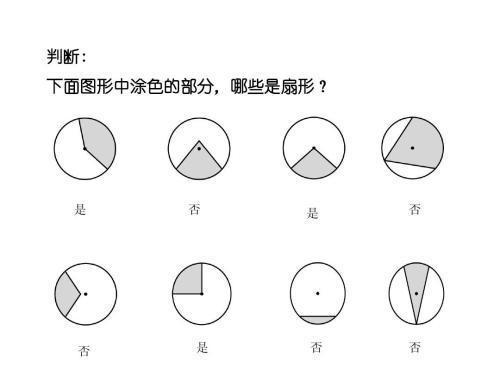



数学 扇形面积怎么推导来的 定积分求双纽线面积要用到 扇形面积角度积分公式 德涵网
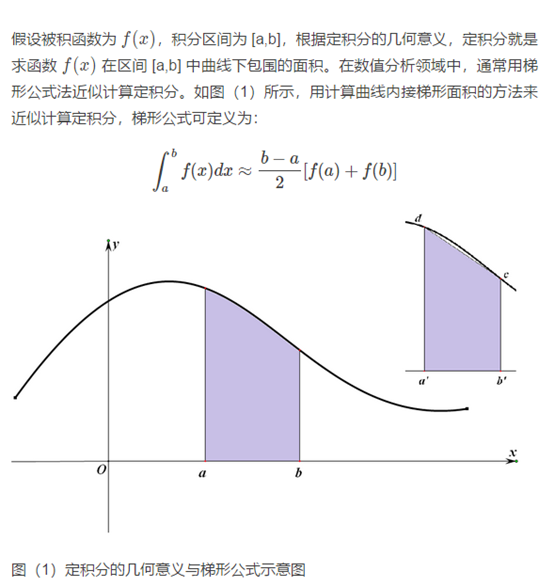



2 3 迭代法计算定积分 Orxx 博客园




圆的面积公式 圆的面积公式是怎么得到的 52fmz购物网




椭圆部分面积公式 求椭圆部分面积有没有公式呢 三人行教育网 Www 3rxing Org



1




使用几何法和微积分求相交圆阴影部分的面积 Youtube




曲面的面積 Youtube




第十章定积分的应用 一 一 平面图形的面积面积公式 直角坐标 极坐标 二 由平行截面面积求体积由平行截面面积求体积



积分求平面图形的面积 玄数
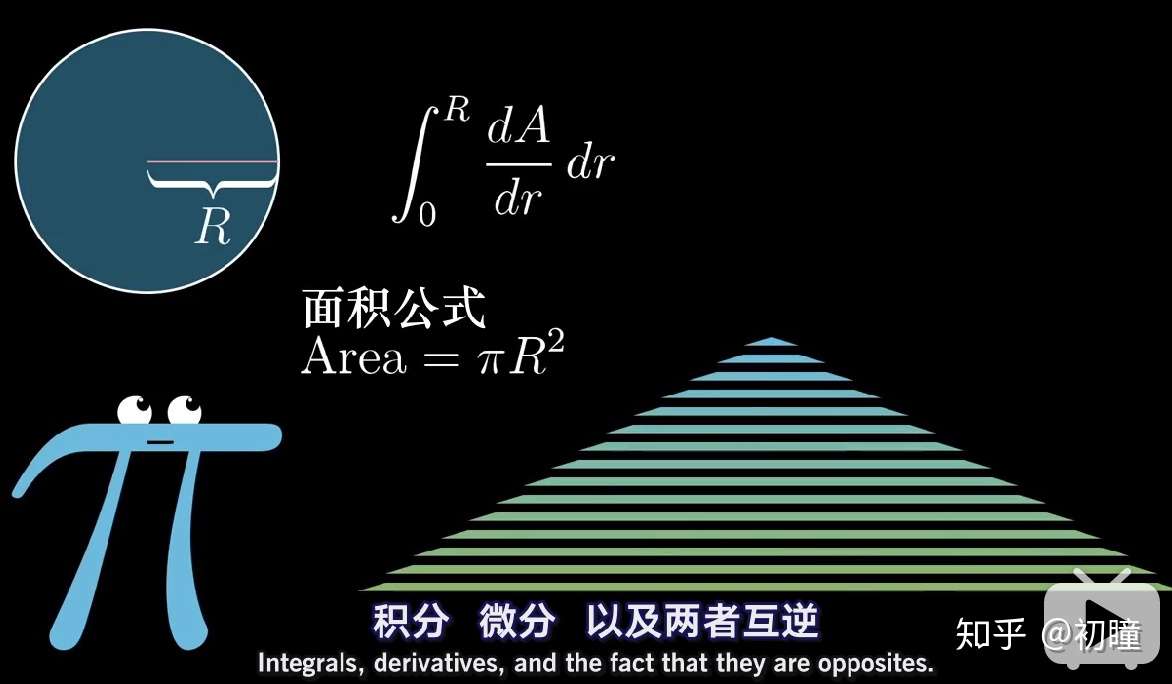



微积分的本质 1 导论 知乎




从三角形面积公式到微积分概念入门 文学城博客




数学 使用积分推导圆的面积公式 一切皆可视 Csdn博客



第十章定积分的应用 一 一 平面图形的面积面积公式 直角坐标 极坐标 二 由平行截面面积求体积由平行截面面积求体积




定积分面积公式 如何用定积分求面积总结一下用到的所有公式 包括极坐 三人行教育网 Www 3rxing Org




センター数学最強 A 6 A 12 A 3面積裏技公式 大学入試共通テスト 受験の月




高等数学 微积分 教你如何简单地推导求导公式 一 海砸的博客 程序员宅基地 微积分求导公式 程序员宅基地




用感覺理解球體表面積公式 Youtube



定积分圆面积公式 定积分圆的几何意义公式 公式学习




微积分怎么求圆面积公式




梯形公式 維基百科 自由的百科全書




定积分求面积步骤 百度经验
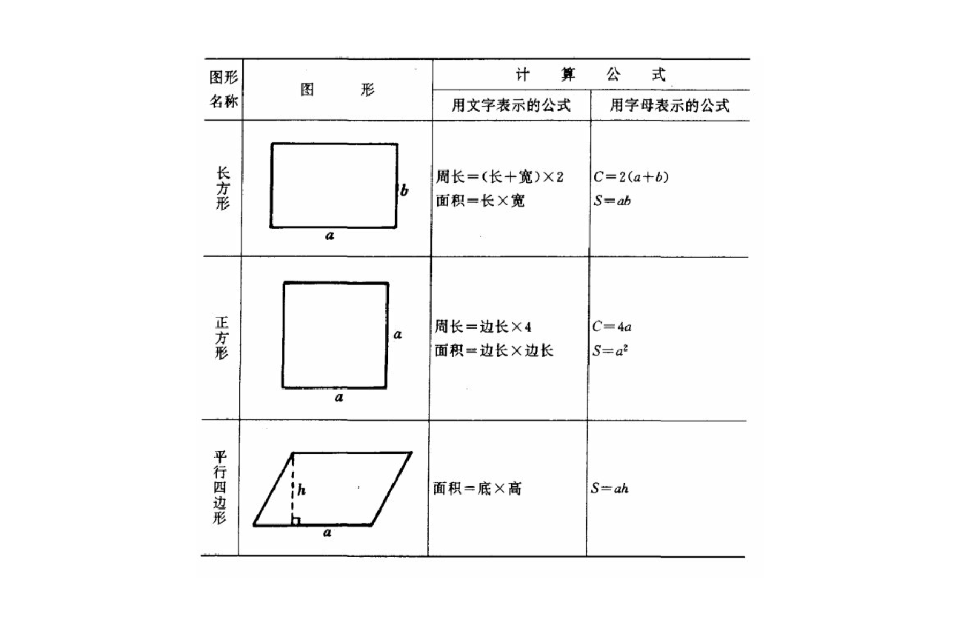



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



用第二型曲线积分求椭圆的面积 作业 慧海网
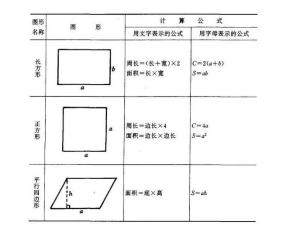



面积公式 搜狗百科




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科
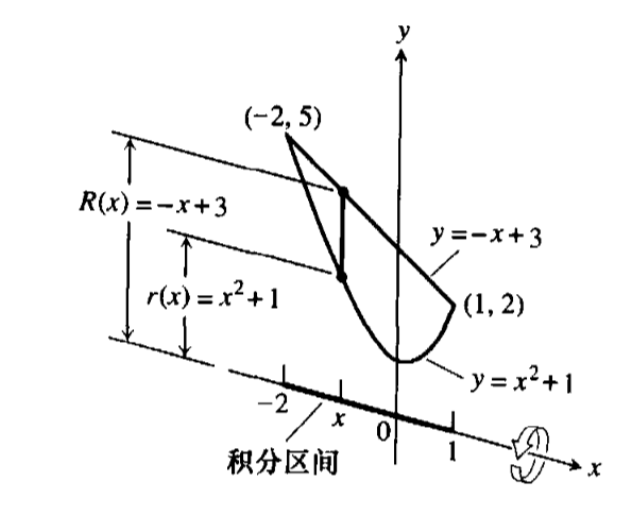



积分计算曲线围绕x轴旋转形成的立体体积 Zhang Phil Csdn博客 绕x轴旋转体体积公式
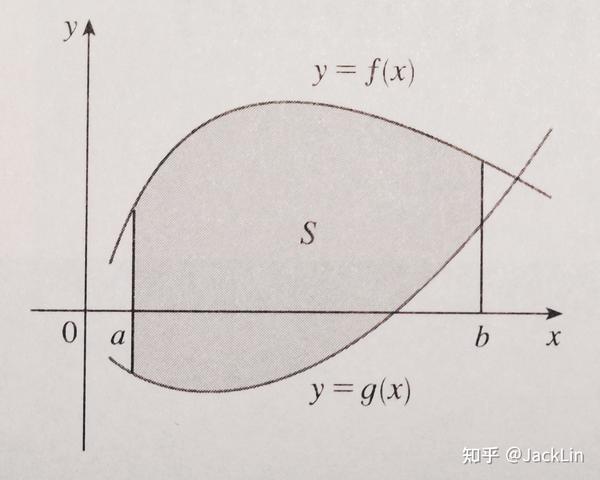



微积分怎么求曲线面积 微积分求面积例题 定积分求抛物线面积



心形线面积计算为什么是a 2 1 2r 2dv18 心形线面积公式推导 崇爱网



椭圆面积计算公式 椭圆面积计算公式画法




橢圓面積證明法 心中的科學 科學的探索 探索的心中 隨意窩xuite日誌
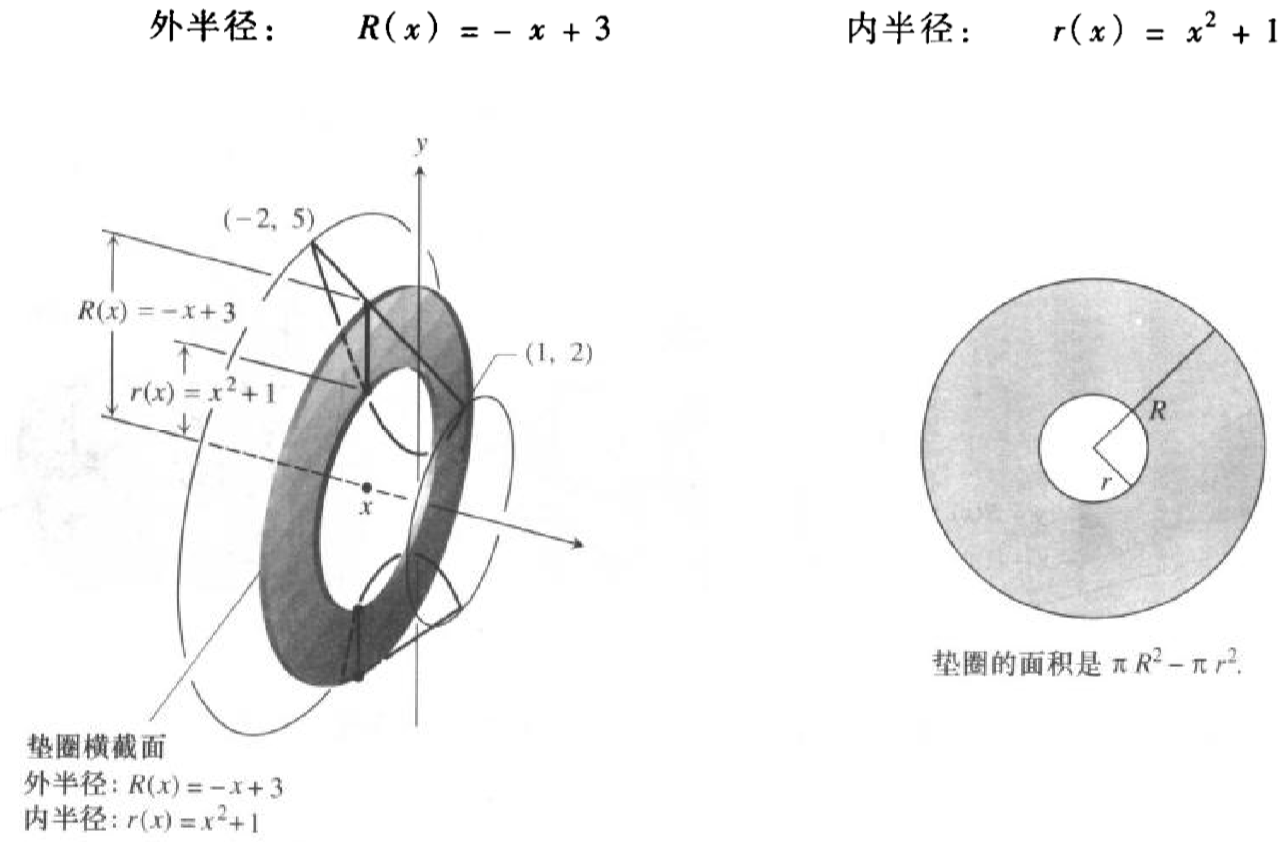



积分计算曲线围绕x轴旋转形成的立体体积 Zhang Phil Csdn博客 绕x轴旋转体体积公式




微积分 极限思想推导圆周长 面积公式下载 Word模板 爱问共享资料
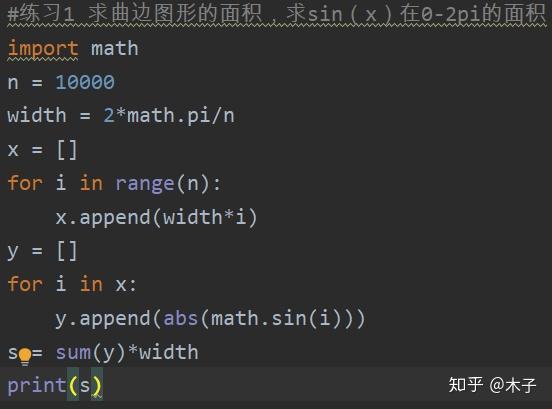



定积分求曲边三角形面积 曲边三角形公式 曲边三角形面积积分公式




简单解法版 计算红色部分的面积 初中知识近似解法 不用定积分通用公式解法 哔哩哔哩




椭圆的面积公式周长公式二重积分推导过程详解 计算机器在线计算



使用数学中的微积分推导出圆的的面积公式a Pr 2 哔哩哔哩 Bilibili




你也能懂的微积分 上 牛顿 微分 导数 定理 网易订阅



定积分求面积公式图片 表情大全



漫步微积分7 2 两条曲线间的面积 Burningbright




极坐标表面积公式 二重积分求球面积用极坐标表示 三人行教育网 Www 3rxing Org



按对面积的曲面积分的定义证明公式 Ss S F X Y Z Ds Ss S 1 F X Y Z Ds Ss S 2 F X Y Z Ds 其中s是由s 1 和s 2 组成的数学竞赛平台



圆环面积公式与勾股定理 Matrix67 The Aha Moments




圆的面积公式怎么来的 李永乐老师4分钟带你了解微积分基本原理 Youtube



1



曲线侧面积积分公式 如何用微积分推导出圆锥的侧面积公式s Prl 三人行教育网 Www 3rxing Org
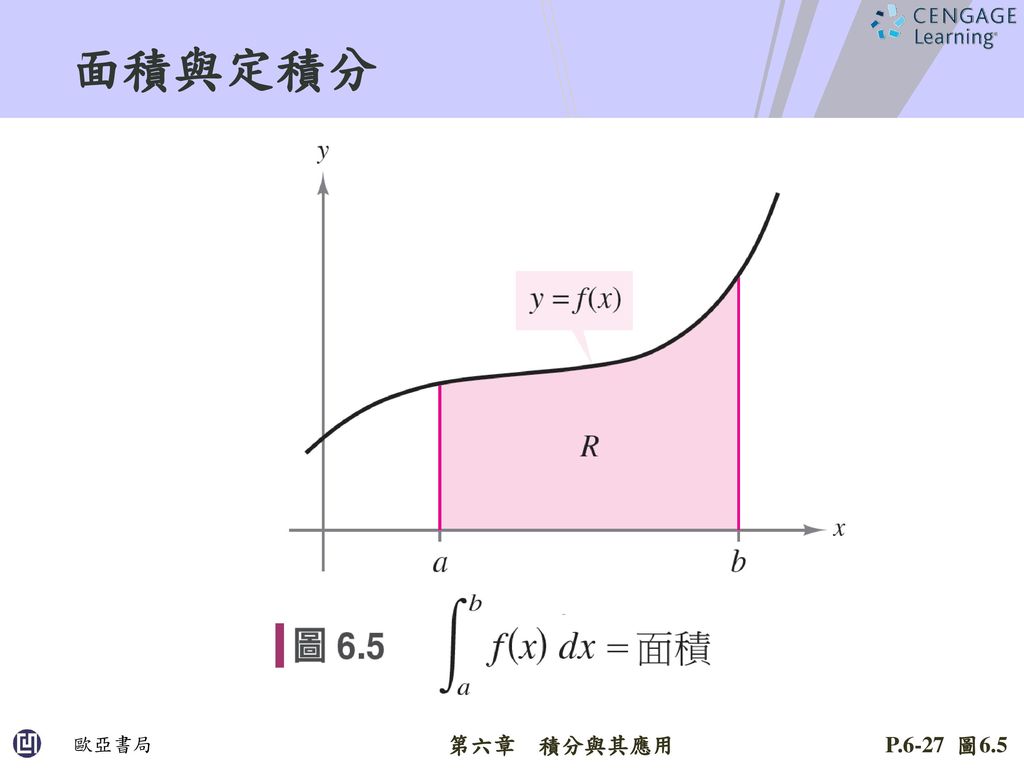



6 4 面積與微積分基本定理 Ppt Download
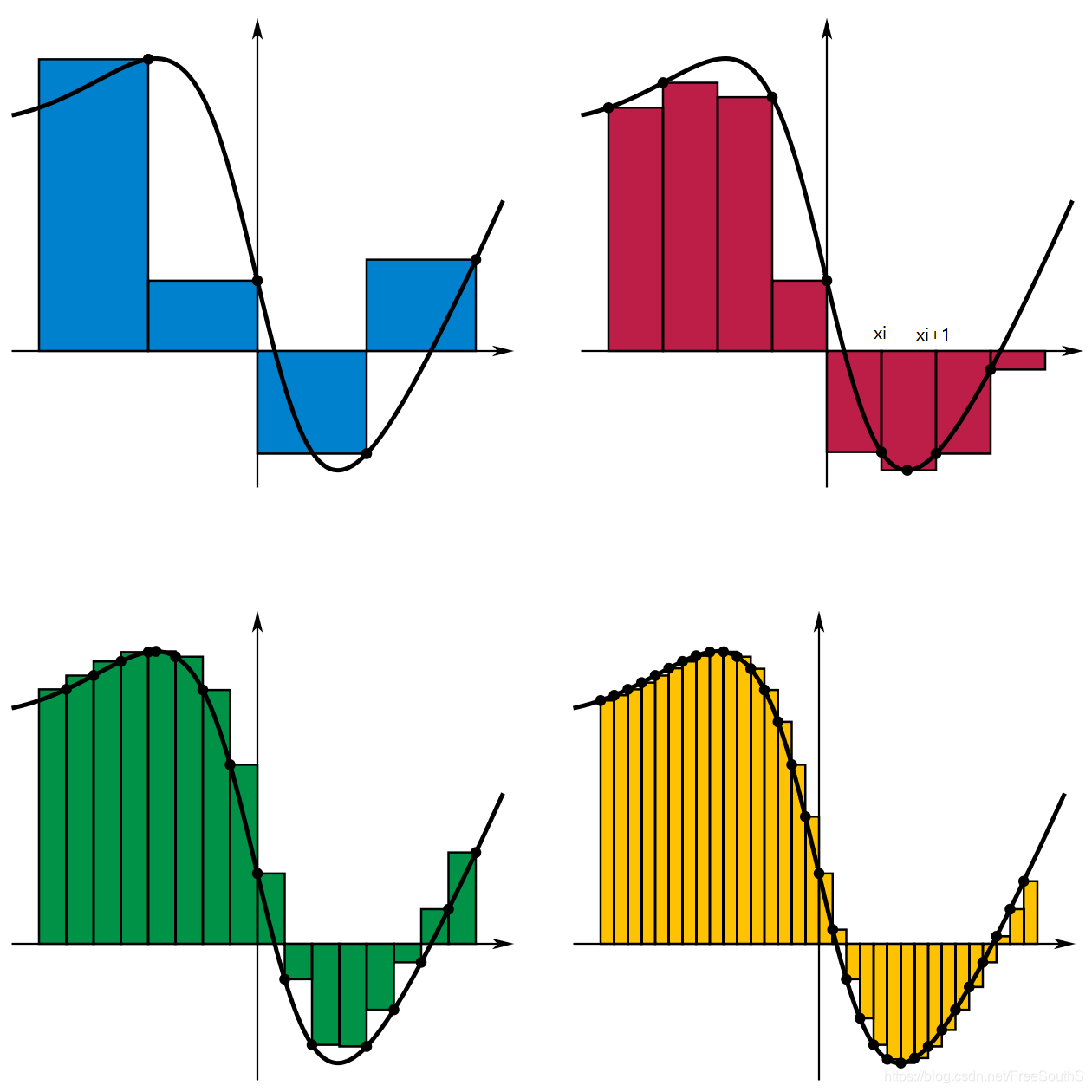



数学 积分 Integration 的定义 黎曼和 黎曼积分 牛顿 莱布尼茨公式 微分三大中值定理 一切皆可视 程序员宅基地



积分求平面图形的面积 玄数




面積分體積分向量積分 高斯定理與連續方程式 Dwfne
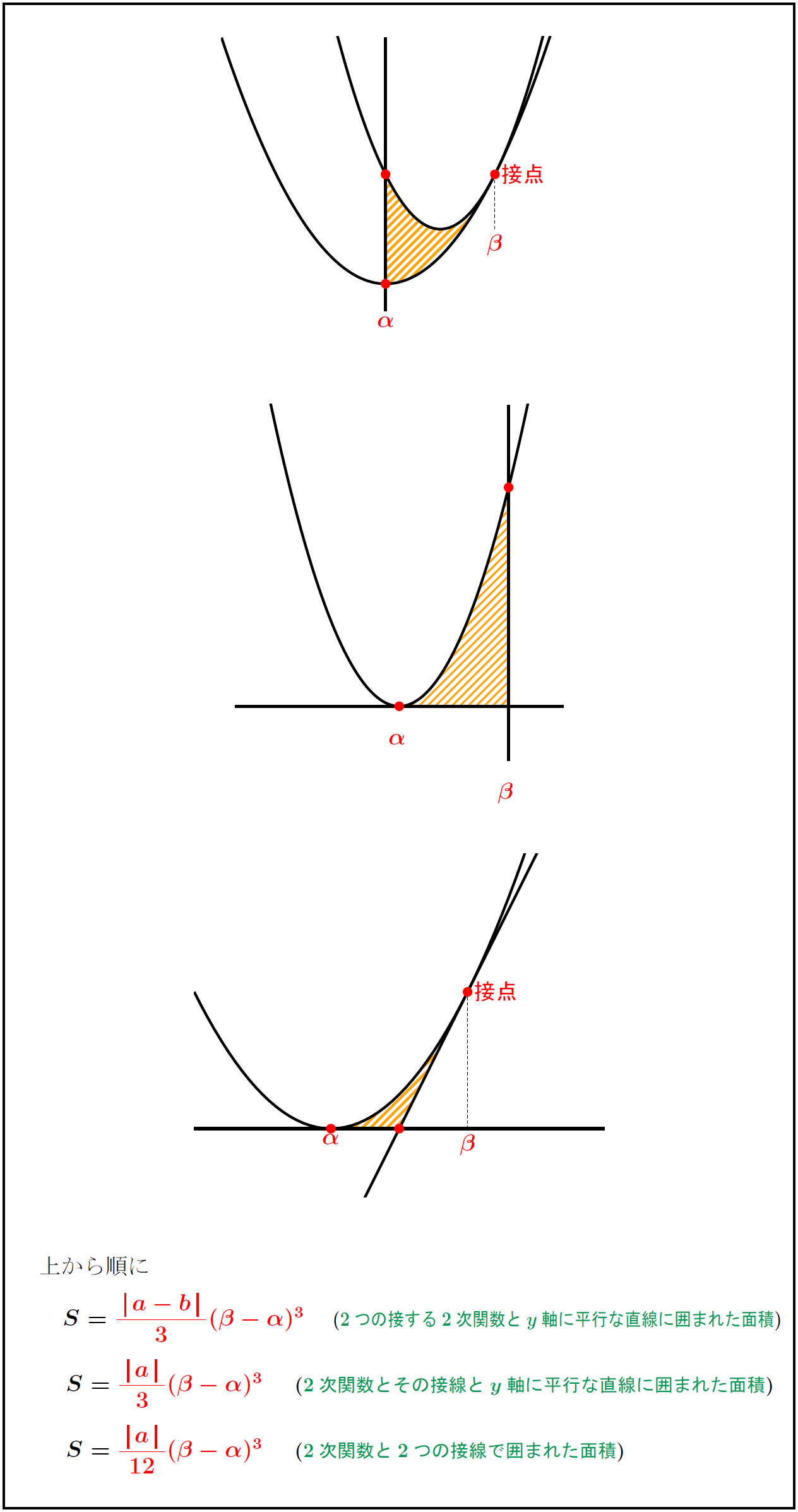



センター数学最強 A 6 A 12 A 3面積裏技公式 大学入試共通テスト 受験の月




如何以圓面積公式推導出橢圓面積公式 你想到了簡單的方法嗎 每日頭條




高等数学重积分 Jason S Blog



Ai产品经理需要了解的微积分通识 人人都是产品经理



积分微分的本质 犀牛的博客



数学笔记27 极坐标下的面积 我是8位的 Csdn博客 极坐标求面积
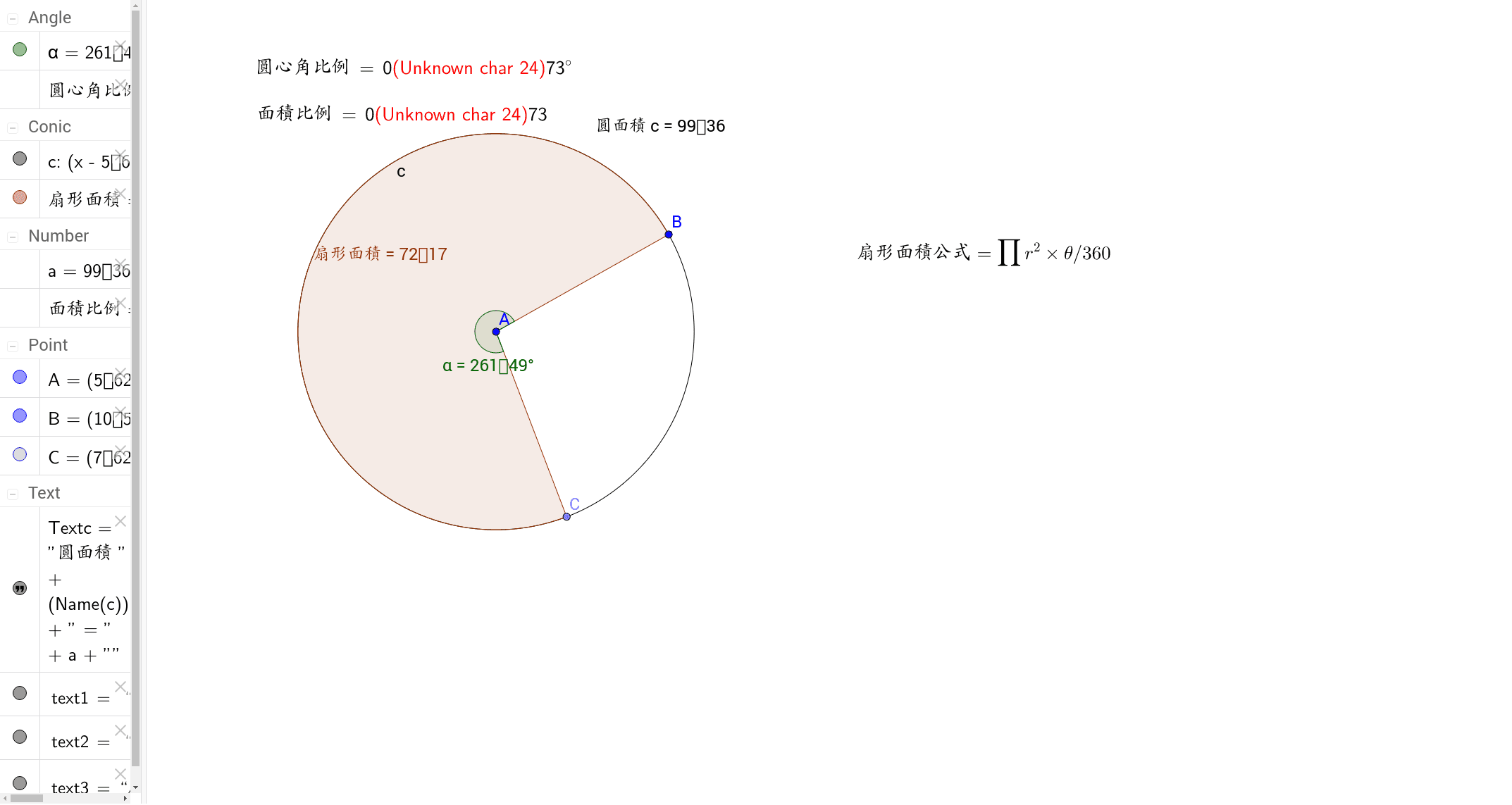



扇形面積公式 Geogebra



数学笔记13 定积分 我是8位的 Csdn博客




Andrew Liu 文学城博客




如何用微积分求解球体 椭球体 圆锥的体积 旋转体体积公式推导 网易订阅



定积分面积公式 表情大全
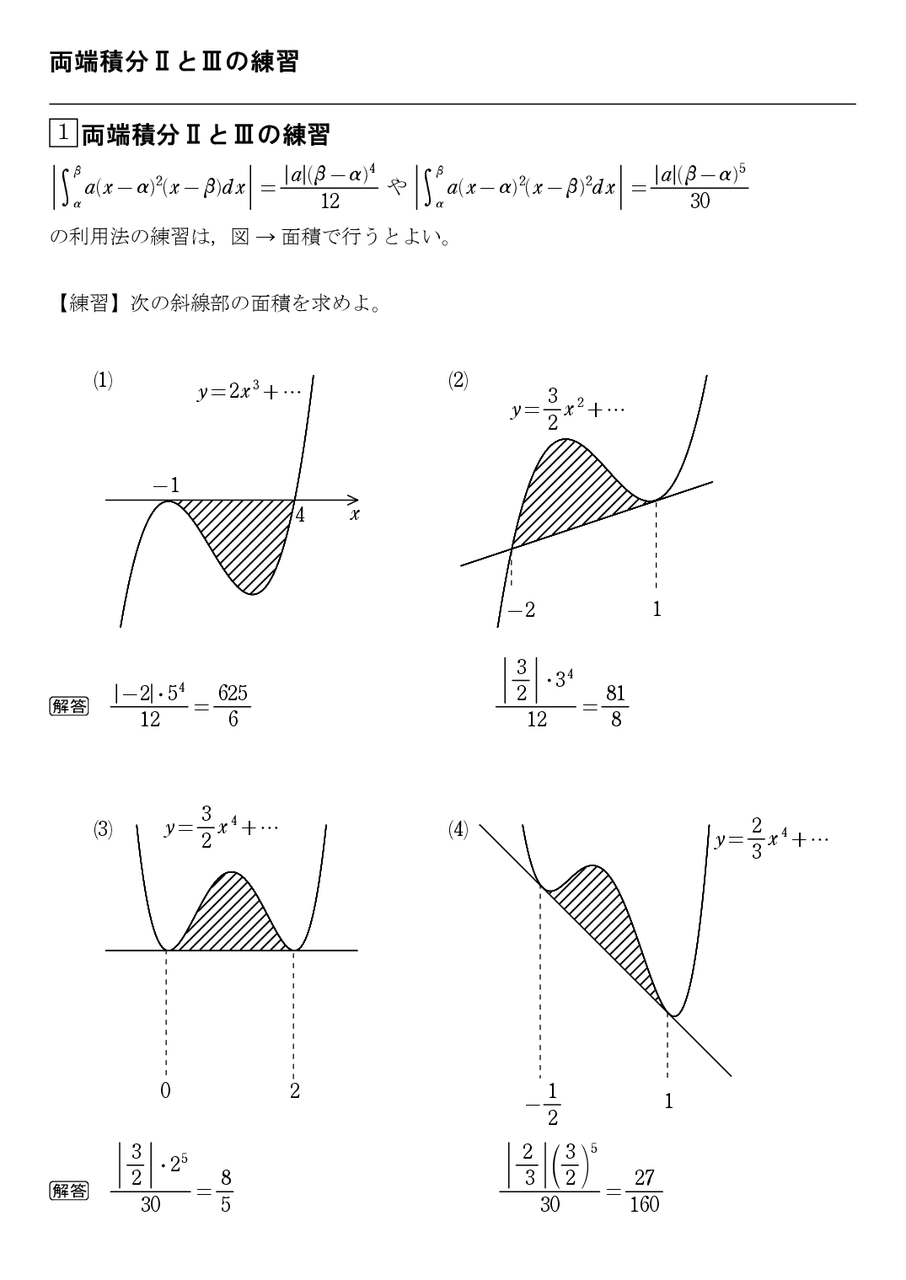



積分の面積公式 5 両端積分 の利用法 怜悧玲瓏 高校数学を天空から俯瞰する



Www Matongxue Com Madocs 251




最漂亮与最实用的微积分公式 微积分第一 第二基本




積分 面積 裏技公式 早見チャート 高校生 数学のノート Clear



C 实现定积分求解 Alex S Blog




弧长公式扇形面积公式积分极坐标高数推导过程 小街网




积分公式 搜狗百科




高等数学入门 利用二重积分计算平面图形面积 百度经验




极坐标下 定积分求面积公式推导 知乎



数学笔记27 极坐标下的面积 我是8位的 Csdn博客 极坐标求面积



单变量微积分笔记16 定积分的应用1 对数与面积 我是8位的 博客园



D 44 定积分的解法 黎曼和估算与面积法 知乎




定积分求曲线面积公式 定积分求面积例题 定积分求旋转体体积




定积分面积公式 如何用定积分求面积总结一下用到的所有公式 包括极坐 三人行教育网 Www 3rxing Org



弧形面积公式 西瓜视频搜索



Www Matongxue Com Madocs 8



定积分面积公式 表情大全



センター数学最強 A 6 A 12 A 3面積裏技公式 大学入試共通テスト 受験の月



圆的面积公式 圆的面积公式画法



高等数学 简单直观地了解定积分 Coder梁 博客园




球体表面积推导定积分 怎么用定积分证明球体表面积公式 三人行教育网 Www 3rxing Org



用定积分求面积的两个重要公式 1 4定积分与微积分基本定理 高中人教b版 数学中国网



微积分到底有多神 能完成多少不可思议 难以测量的计算 他简直强大的让人害怕 知乎



1



0 件のコメント:
コメントを投稿