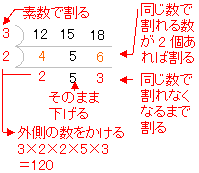
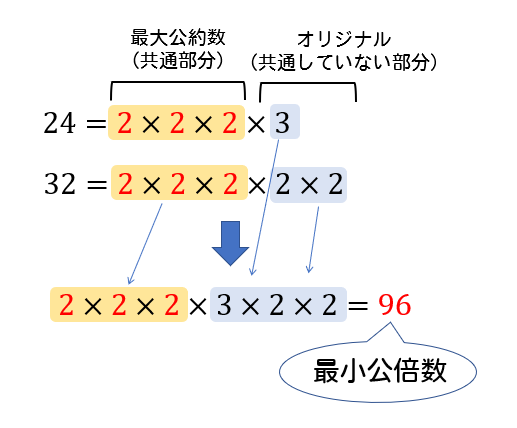
最小公倍数の求め方 2つの正の整数 a , b の最大公約数(=共通の約数で最も大きいもの)を g 、最小公倍数を l で表すと a=g·a' , b=g·b' ( a' , b' には公約数はない) と書けます。 このとき、最小公倍数は l=g·a'·b' で求められます。約数と倍数 a = kb(a,b,k ∈ Z,b = 0) を満たすkが存在する時bはaの約数、 aはbの倍数 aはbで割り切れるといいb∣aとかく約数 約数ある整数を割り切れることができる整数。 18の約数1、2、3、6、9、18 素数約数が1とその数しかない整数 2、3、5、7、11、13、17、

倍数もしくは約数である関係についての推移律 タロウ岩井の数学と英語 Note
倍数と約数の違い
倍数と約数の違い-「約数」ってなぁに? 「約数」って漢字が並んでて、難しそうだね。 でも、難しそうに見えるだけだから、楽しく考えよう。 「約数」って普段使わない言葉だね。 「約数」は、ある数を割った時に、割り切れる数の集まり のことなんだ。倍数と約数 ①倍数 5を整数倍した数を5の倍数といいます。 ②公倍数 ・3の倍数と4の倍数の共通な数を 3と4の公倍数といいます。 ・公倍数の中で,いちばん小さい公倍数を 最小公倍数といいます。3と4の最小公倍数は




因数分解で大活躍 倍数 約数 の見つけ方
つまり 割り切れる数 です。 例えば、21 ÷ 7 = 3 とは 21 ÷ 3 = 7 でもあるので「 3 と 7 」は「 21 の 約数 」であると言えます。 「 倍数 」とは、 約数から見た時の 「 割られる数 (元の数)約数と倍数についての例題をいくつか紹介していきます。 例題 (倍数の利用) a、bが整数だとすると、ab、bが3の倍数ならば、aは3の倍数であることを証明せよ。 解答 ab、bが3の倍数であるので、整数k、lを使って、 \(ab=3k,b=3l\) と表せる。よって、 令和2年度算数教科書読み比べ (7)~0は偶数だが2の倍数ではない 同じ対象に関する教科書ごとの取り上げ方の違いを知るため,『小学校学習指導要領(平成29年告示)解説算数編』に記載の「偶数,奇数」と「約数,倍数」をチェックしました。 経緯を書い
とかって言わない? この元の量を「2倍」や「4倍」した量が「倍数」なんだ。 別の言い方をすると、 ある数を2倍、3倍、4倍・・・と倍にした数の集まりが倍数 なんだ。 もとの数が「 2 」とすると、 2 ,4,6,8,10,・・・・ なんだ。 もとの数が「 3 」とすると、倍数は、定義 整数 a ≠ 0 が N の約数であるとは、「ある整数 b をとると N = ab が成立することである」であるが、条件「 a ≠ 0 」を外すこともある。 このときは、 N = 0 のときに限り 0 も約数になる。 約数が無数にある整数は 0 だけである。 負の符号は本質的な問題ではないため、ここでは以下現れる第1回 倍数と約数 倍数と約数の基本的な求め方について、 5年上第1回では教えてくれていません。 4年下第1回「倍数」・第2回「約数」で学習済みということなのでしょうが、 最重要項目なので確認しておきます。 倍数の定義 の倍数= の段の九九
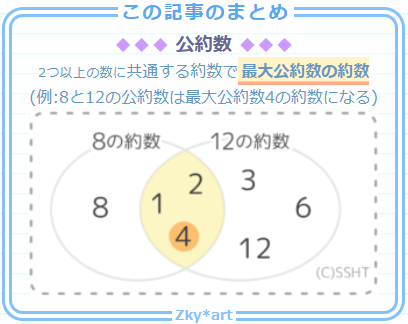
精選版 日本国語大辞典 公約数の用語解説 〘名〙① 数学で、二つ以上の整数に共通な約数。最大のものを最大公約数という。整式に対しても準用する。公因数。〔数学ニ用ヰル辞ノ英和対訳字書(18)〕② 比喩的に、二つ以上のものが共通して有している要素。まずは倍数と約数とは何か,ということについておさらいしていきます。 倍数 とは, ある数字を 0倍,1倍,2倍,3倍,・・・と 整数倍していった数の集まり のことを指します。 例えば2の倍数は0,2,4,6,・・・というようになります。(1)48の約数は全部で 個あります。 (2)50以上の素数で2番目に小さい数は です。 (3)255、459、1122の最大公約数は です。 (4)36、60、84の最小公倍数は です。 (5)2けたの整数で、6の倍数で144の約数でもあるのは 個あります。




小5 算数 小5 倍数 約数の文章題 Youtube



最大公約数と最小公倍数
小学5年生 8月の算数プリントは、 「約数と公約数」「公倍数・公約数の利用」 の練習問題です。 プリントの問題番号の横に付記している「難」と「やや難」の表示は、下記の難易度を表しています。 難 栄光ゼミナール生徒の正答率が 50%未満の倍数・約数 2つの整数a,bがあって, a=b×q (qは整数) のとき,aはbの倍数,bはaの約数として定義されます。 小学校では,一度に両方の概念を与えると混同しやすいので,別々に扱います。 それで,倍数については,下の例のように,具体的な数をあげてやまぐちっ子 学習プリント 倍数・約数 ステップ2 月 日 次の文章を完成させましょう。 8をわり切ることのできる整数を,8の といいます。 8の約数は, , , , の4つです。 約数を で囲みましょう。 3の約数 123 4の約数 1234 6の約数




競プロ 素因数分解と約数と倍数 なかけんの数学ノート
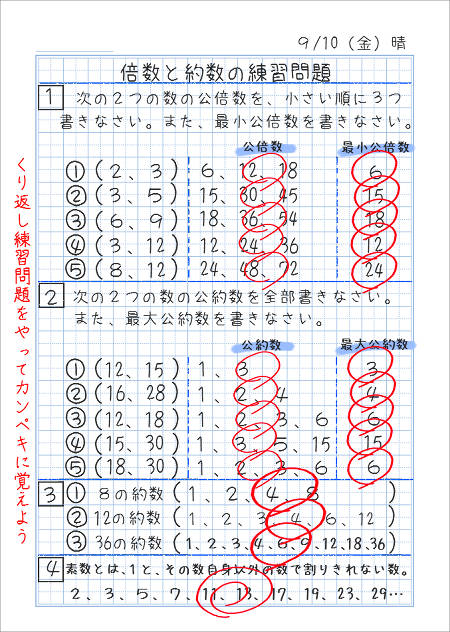



公約数と公倍数の自主学習ノート例 家庭学習レシピ
めざす姿は 倍数や約数の求め方を説明できるようになりましょう。 (1)倍数について答えましょう。 ①3の倍数を小さい方から7つかきましょう。 ②かいた3の倍数を偶数と奇数に分けましょう。 ③3と7の公倍数を小さい方から2つかきましょう。このように,約数や倍数,因数分解は,定数倍の違いを除いて決まる. の中で,0でない定数は逆数もまた整式である. 逆数もまた整式となるのは0でない定数にかぎる. つまり では0でない定数が単数数の性質といってまず頭に浮かぶのは「約数と倍数」でしょう。 「約数と倍数」は、5年生で基本を習った後、 再び6年生の2月に学習することが多いようです。 ということで 「6年生になると、5年生のときと何が変わるか」 をみておきましょう。




小学生 3つの数の最小公倍数 最大公約数の求め方 特殊なすだれ算も図で解説 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算
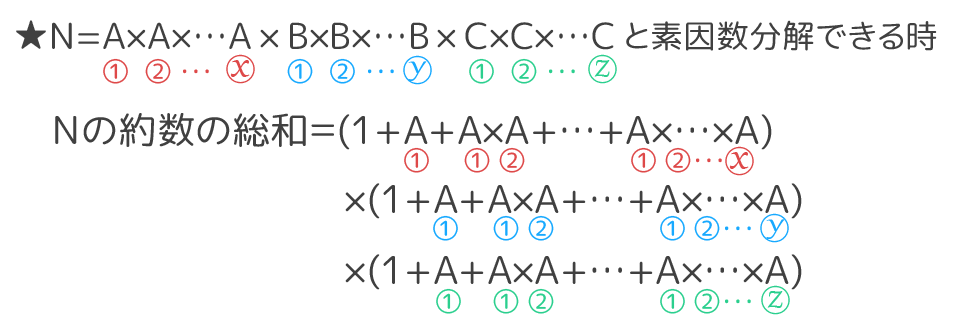



約数の総和の求め方 そうちゃ式 受験算数 新1号館 数論 特殊算
倍数とは?1分でわかる意味、計算、3と8の倍数、公倍数との違い 約数とは?1分でわかる意味、4や6の約数、計算、求め方、最大公約数との関係 公倍数と最小公倍数の違い 公倍数と最小公倍数の違いを下記に示します。 公倍数 ⇒ 2つ以上の整数に共通するたとえば、小学生が苦手とする分野に約数・倍数があります。 この分野で苦戦している生徒に聞いてみましょう↓ 「約数」と「公約数」と「最大公約数」の違いは? 多くの生徒は、ここで頭を抱えるは gcfとlcmの違いは、2つの用語の定義と意味です。 2組の数の公約数を計算すると、そのように作成された約数のリストから、これら両方の数の最大公約数を簡単に確認できます。 lcmは、与えられた数値のセットから計算できる最小公倍数です。 略語と




中学受験 算数 動画解説 倍数と約数 最大公約数と最小公倍数 応用問題 Youtube




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算
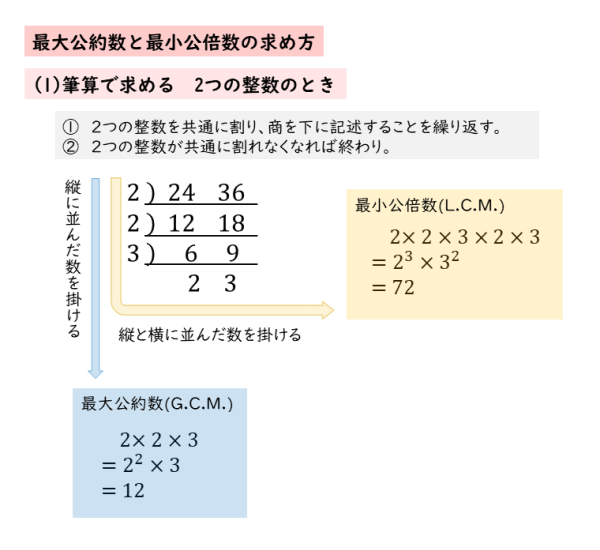
約数と倍数を理解し,そしてそれらをみつける方法を学びます。 これらのビデオをマスターしたら,小数を学ぶ準備ができています。 カーン アカデミーは誰にでも,どこにでも無料で世界クラスの教育を提供することを使命としています。 0は偶数か、2の倍数か、整数か Togetter 思うことあって一昨日の朝に書き溜めてツイートし,Togetterにしました. 算数で0を倍数に入れないのはなぜかを書いた時点で,この件は一応これでいいかなと思っていたのですが,連ツイをした前の日に,1年前に発した以下の内容に対して,お気に入り最大公約数,最小公倍数とは 2つ以上の正の整数に共通な約数(公約数)のうち最大のものを最大公約数といいます. 例 12 と 18 の公約数は, 1,2,3,6 で, 6 が最大公約数 2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを最小公倍数といいます.




倍数と約数 ート 5年生ワークシ 小学校 24と36の公約数 2 4 6 8 10




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
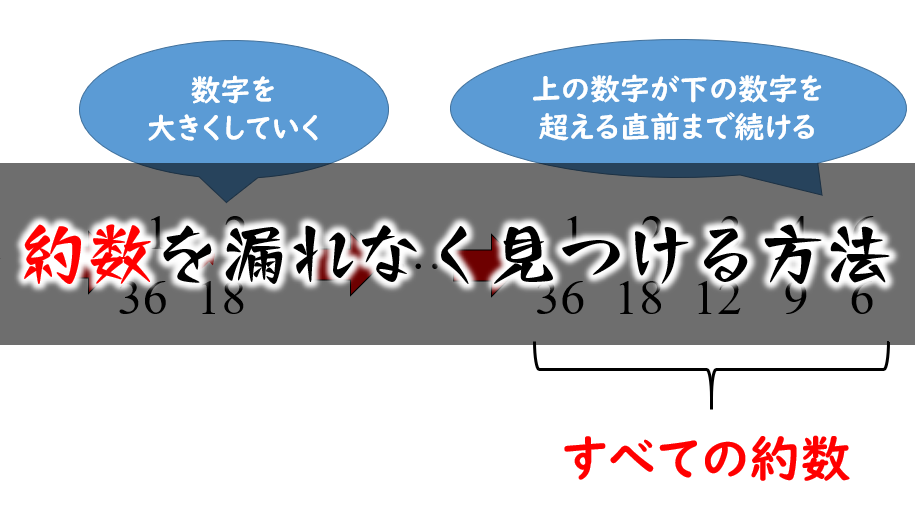
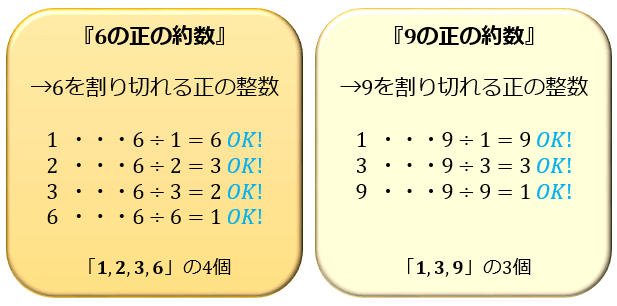
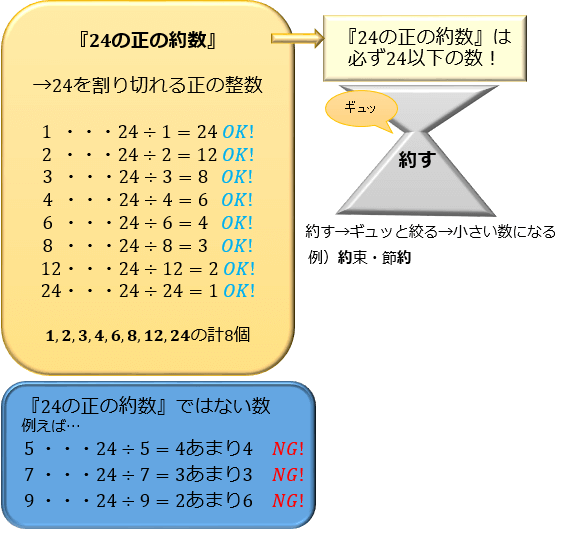
約数とは 「 ある数を割ったときに割り切れる数 」をもとの数の約数といいます。 倍数と違って約数は、数字ごとに個数が決まっています。なので、すべて書き出すことができるのです。 18の約数だったら、1,2,3,6,9,18 の6個となります。5年算数整数 教え方のポイント ① 偶数と奇数の意味 ② 倍数・公倍数・最小公倍数の意味と求め方 ③ 約数・公約数・最大公約数の意味と求め方 ④ 生活場面で整数の性質を使うことA を整数に限ると、 a の倍数とは「 a で割り切れる整数」のことであり、 a の 約数 (「 a を割り切る整数」)と対比されることも多いが、倍数は a が整数でなくても定義できる。 倍数の中で 0 以外は 符号 の違いだけの組が現れるので、 0, ±a, ±2a, ±3a,




倍数と約数 公約数と最大公約数 Youtube




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
−3a, −2a, −a, 0, a, 2a, 3a, を指す。 a ≠ 0 ならば、 a の倍数は無数に存在する。 a を整数に限ると、 a の倍数とは「 a で割り切れる整数」のことであり、 a の約数(「 a を割り切る整数」)と対比されることも多いが、倍数は a が整数でなくても定義できる。 倍数の中で 0 以外は符
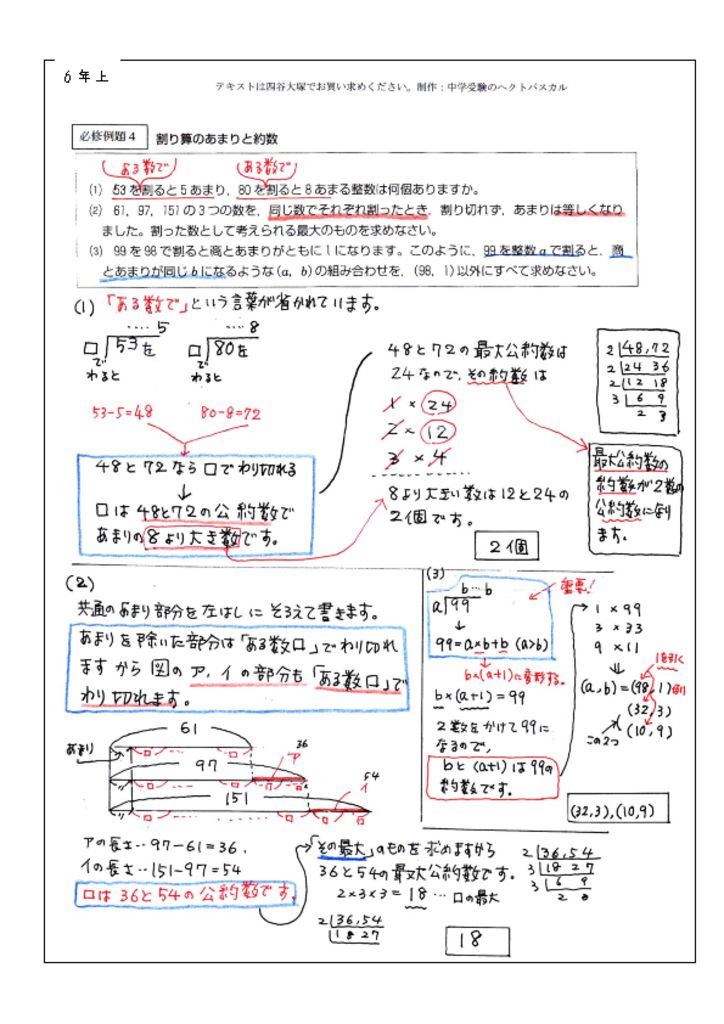



割り算のあまりと約数 数の問題 中学受験の算数 理科ヘクトパスカル




割り算のあまりと約数 数の問題 中学受験の算数 理科ヘクトパスカル




高校数学a 最大公約数と最小公倍数の定義 受験の月



倍数と約数まとめ
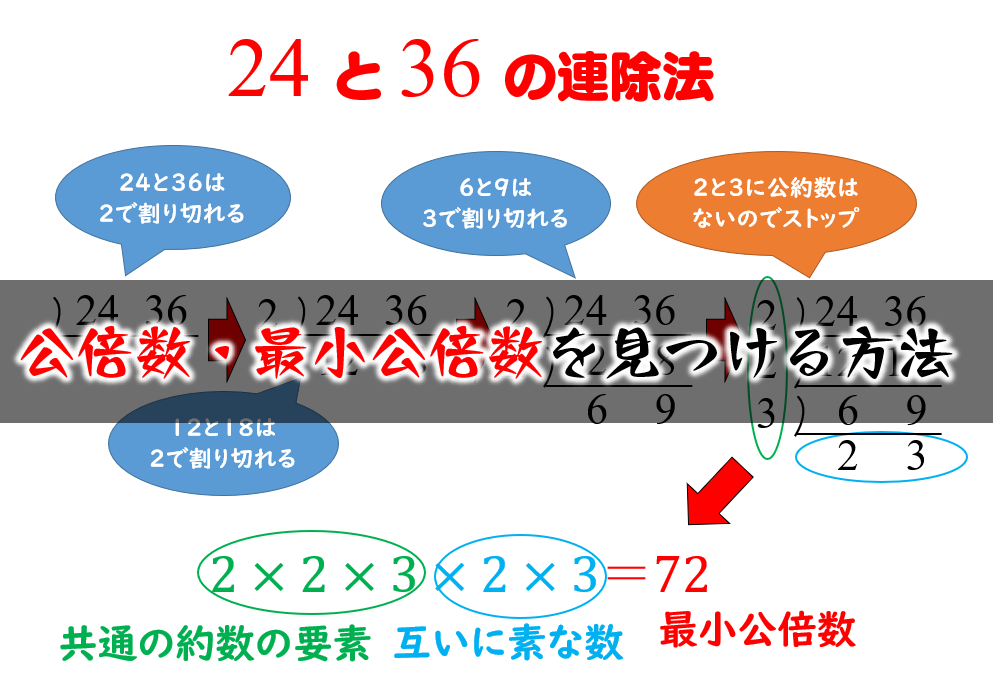



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算



倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support




よりくわ数学a 約数と倍数 教科書より詳しい高校数学




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



約数 倍数




最小公倍数と最大公約数の式 倍数 約数シリーズ Youtube



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



プリント 6年算数 約数と倍数 を作成しました おっくうの教材作成日記 楽天ブログ




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ



約数を漏れなく簡単に見つける方法 小学生でも素因数分解ができると便利 数学fun




約数を学ぼう 倍数 約数シリーズ Youtube




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




新企画 合判模試の準備をしよう 基礎編 倍数 約数 受験情報ブログ 首都圏模試センター




5400の正の約数の中で 30の倍数の個数を求めなさい Clear




因数分解で大活躍 倍数 約数 の見つけ方




倍数と約数 ート 5年生ワークシ 小学校 24と36の公約数 2 4 6 8 10




2 Sqrt3 Descubre Como Resolverlo En Qanda




小5 算数 小5 約数 公約数 最大公約数 Youtube




公約数 最大公約数 公倍数 最小公倍数 求め方 ぐらたん塾



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質



約数と倍数の違い 約数と倍数の違いを教えてくださいできれば 約数の求め Yahoo 知恵袋



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ




倍数と約数 最小公倍数を求める 3つの数 Youtube




約数と倍数 素数と素因数分解




倍数と約数の教え方 2 公倍数と公約数は小さな数のかけ算の形にしてみる ママのための受験算数の教え方プチ講座 中学受験ナビ
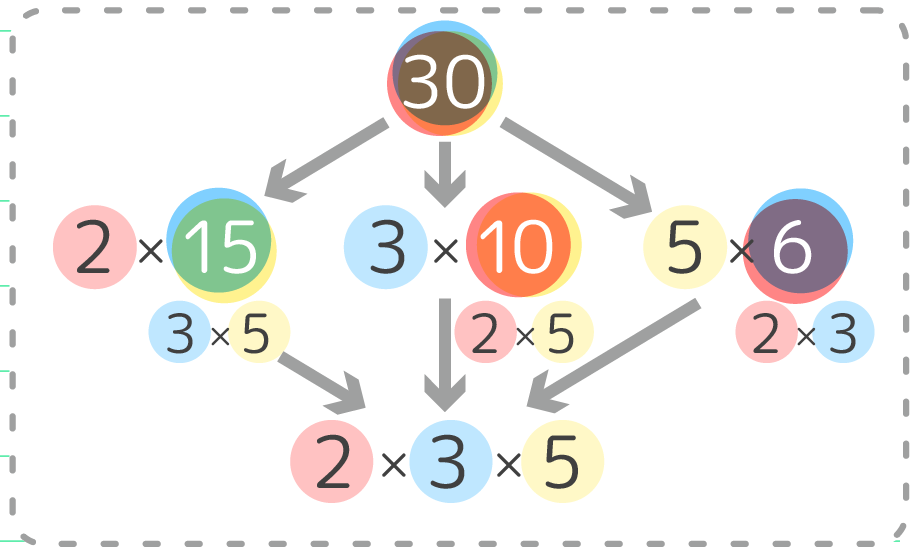



中学受験 素数 約数と すだれ算 での素因数分解のやり方 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算




Lcm最小公倍数 Gcf最大公約数の英語表現を覚えよう ゆう アメリカ生活終了 英語勉強



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




第回 数の性質 約数と倍数 分数 6年生 日能研の歩き方




倍数と約数 最大公約数を求める 練習問題 Youtube




倍数と約数




算数4年から6年



倍数と約数 わり算のあまりと等差数列




高校数学 数a 5 場合の数 正の約数編 Youtube



約数と倍数の違い 約数と倍数の違いを教えてくださいできれば 約数の求め Yahoo 知恵袋




倍数もしくは約数である関係についての推移律 タロウ岩井の数学と英語 Note




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
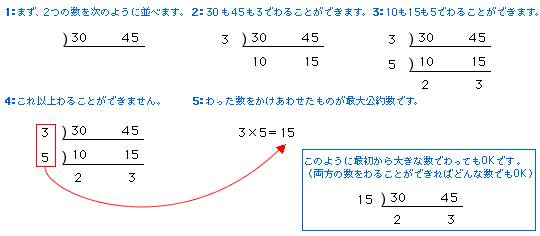



約数 公約数 最大公約数 算数の教え上手 学びの場 Com




似たような問題ですが こちらも で頭がいっぱいです どなたかよろしくお願いします Clear




Q 24の倍数で せいの約数の個数が21個である自然数nを求めよ Clear
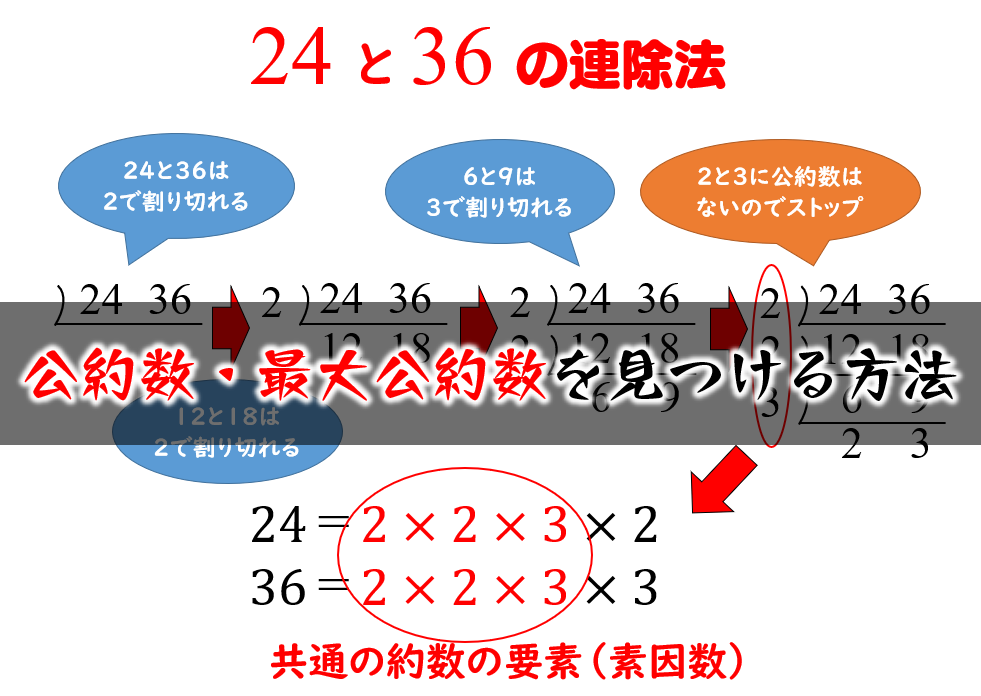



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



倍数と公倍数 周期の問題への応用




小5 算数 小5 20 倍数 約数の文章題 Youtube




倍数と約数再び 正しい理解のために 身勝手な主張



倍数約数 公倍数公約数 そうちゃ式 分かりやすい図解算数 別館




倍数 最小公倍数と約数 最大公約数を教えてみた 妹z会中学受験コース4年



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



5年の算数ソフト 倍数と約数 さくら社




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




倍数と約数再び 正しい理解のために 身勝手な主張



問題文は 24の倍数で正の約数が15個であるような自然数を求めよ という Yahoo 知恵袋



3




倍数表 約数表 石原清貴の算数教育ブログ



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ




倍数 約数 算数用語集



5年家庭学習



Studydoctor約数 倍数とは その求め方 Studydoctor



ドリルズ 小学5年生 算数 の無料学習プリント算数 倍数と約数



2




競プロ 素因数分解と約数と倍数 なかけんの数学ノート




倍数と約数 小5 公倍数 公約数 手探るは最強の解き方 算数の教え方教えますmother S Math Happy Study Support



2




倍数と約数 Apps 148apps




素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算




公倍数公約数に問題なんですが どうやって約数と倍数が分けられるのか分かりません 教え Clear



5年算数整数 教え方のポイント
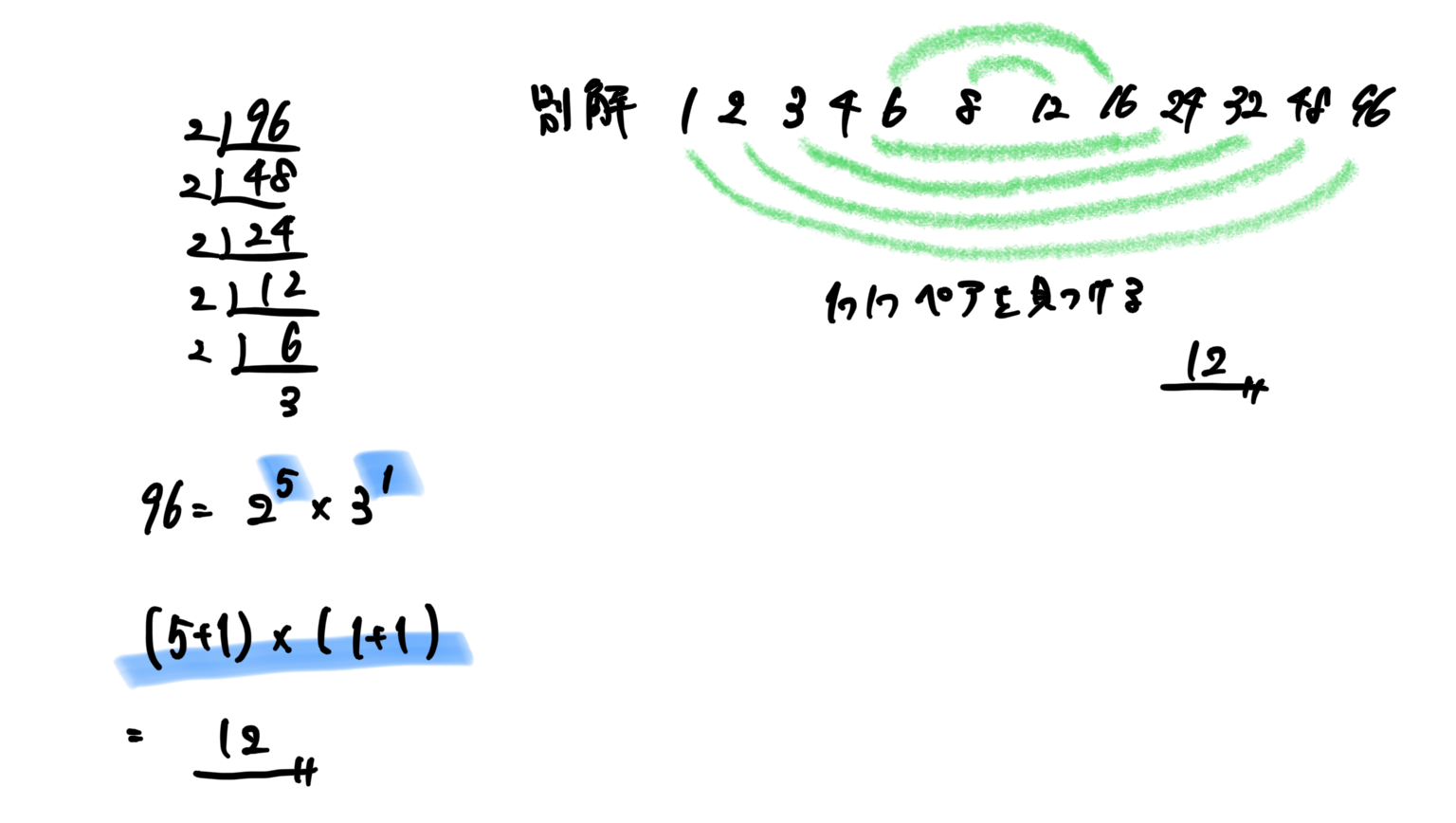



中学受験 約数 倍数 等差数列 周期 受験 ガチ勢 チート Web問題集サイト
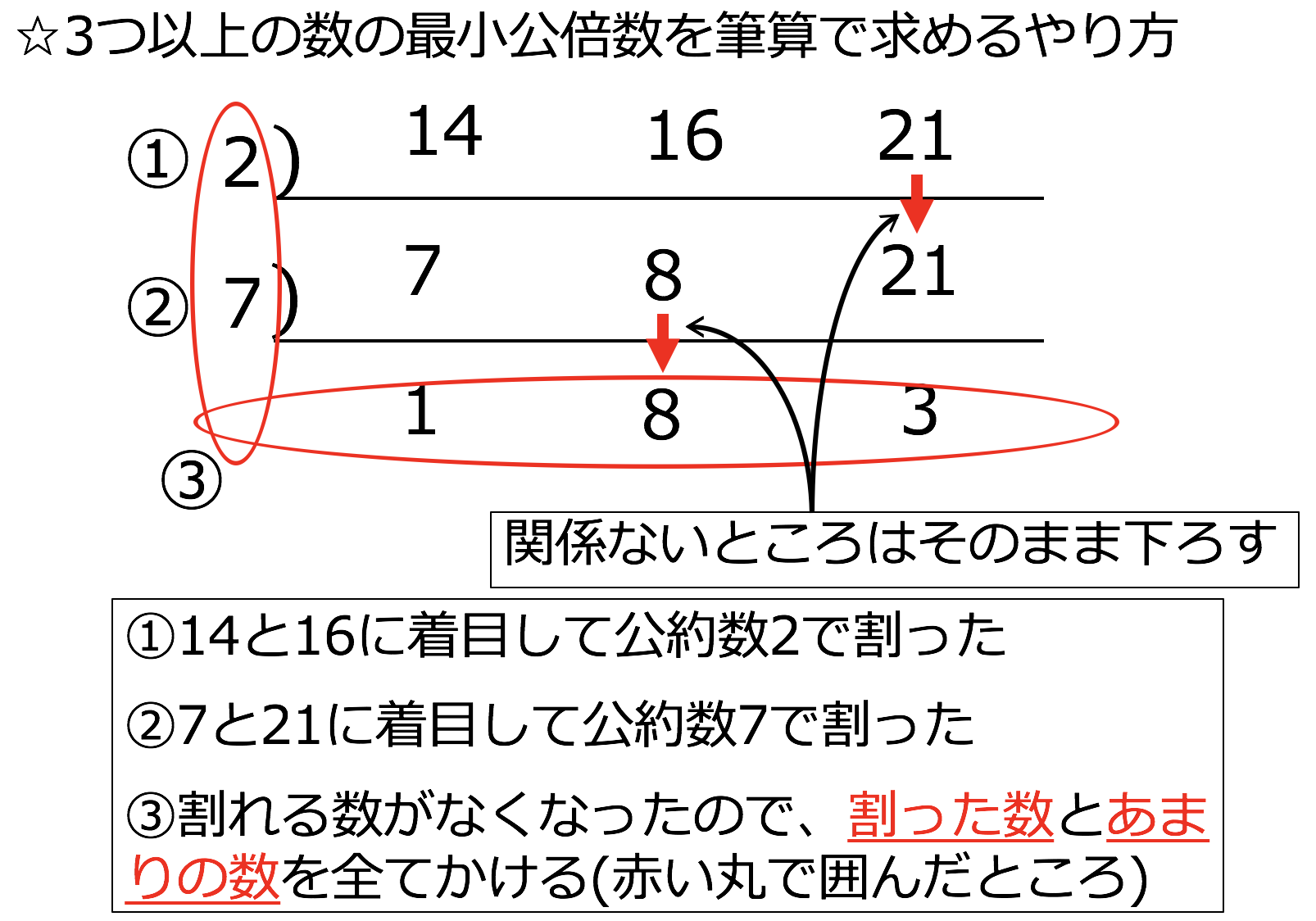



3分で分かる 最小公倍数とは 4通りの求め方も紹介 合格サプリ
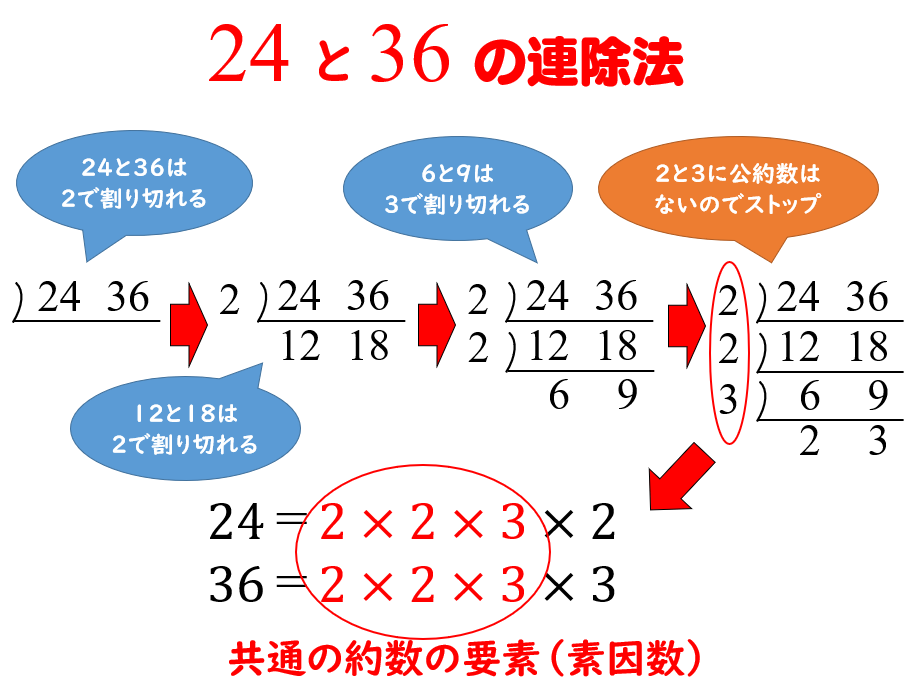



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
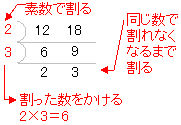



約数 倍数




倍数 約数 算数用語集



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典



3




最大公約数 最小公倍数の求め方 小学生算数指導にも役立ちます 塾講師ステーション情報局




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



小学5年生 倍数 約数と公倍数 公約数とは 分かりやすく総まとめ そうちゃ式 分かりやすい図解算数 別館



倍数と約数 最小公倍数 最大公約数のひみつ シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




倍数と約数について振り返ろう



3




Nitter




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



1



0 件のコメント:
コメントを投稿