四平方定理问题问题描述:给定一个正整数N,这个正整数N可以用不超过4个整数的平方和表示。 例如:12可以表示为 444,返回值 n=3,即 3个4之和。而4是2的平方。 给定整数13,13可以表示为 49, 返回值 n=2,即 2的平方和加上3的平方和。问题分析:这个题目说的实际上的Lagrange四平方定理。三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。平方 平方是一數乘以自己,以下以 5 2 為例說明: 直角三角形
三平方の定理の証明4 直角三角形と内接円 キソカラ
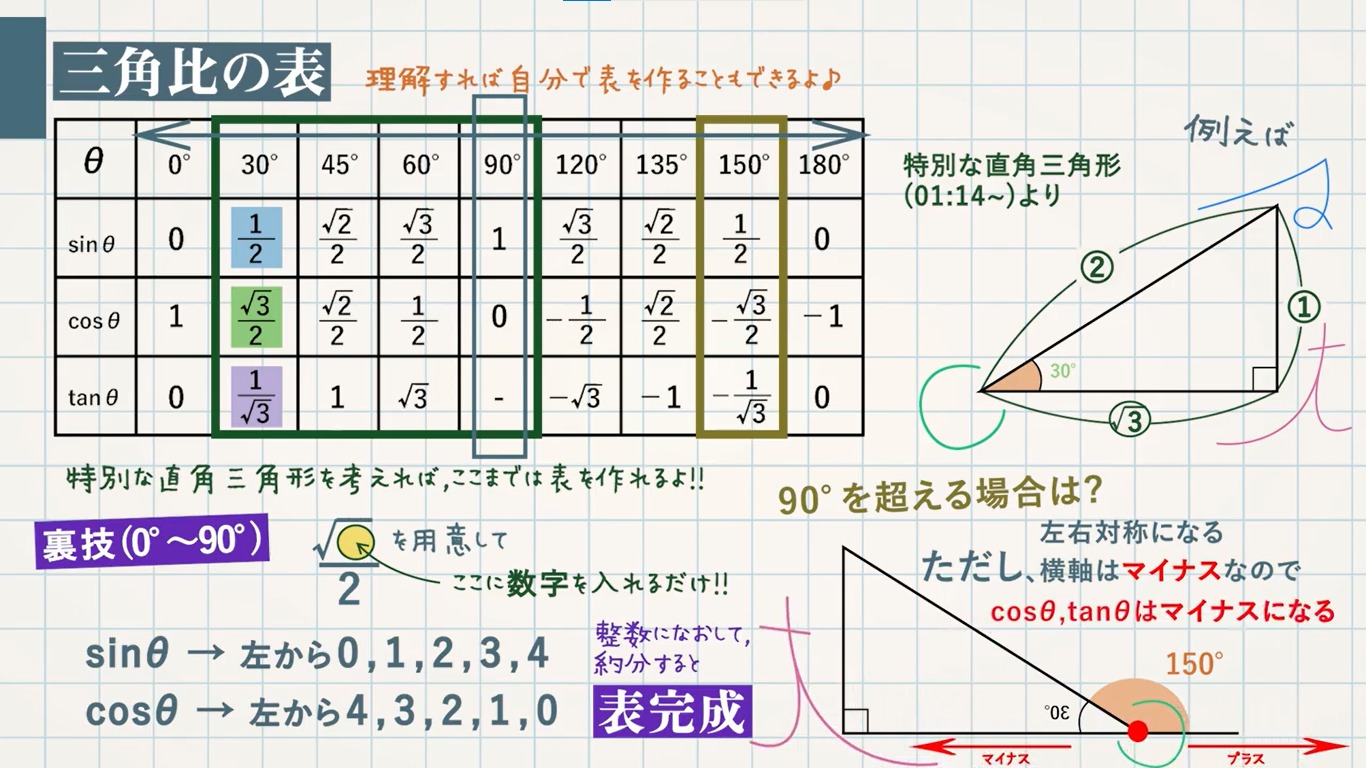
三 平方 の 定理 表
三 平方 の 定理 表-三平方の定理 自動計算サイト 三平方の定理による辺の長さの計算です。 三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 —余弦定理公式要领:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 余弦定理 在余弦定理中,令C=90°,这时cosC=0,所以 c2=a2b2 (1)已知三角形的三条边长,可求出三个内角;




ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル
70以上 三 平方 の 定理 表 リンクを取得;自然数 が三個の平方数の和で表されるための必要十分条件は、,, {,,,,} により、 = () と表されることである。 逆に、 = () で表される自然数は三個の平方数の和で表されない。 これはディオファントスの時代から研究されてきた ことであるが、1798年、ルジャンドルによって証明された。 私の整数好きを決定付けた本があります。水上 勉 (著), 黒川 信重 (監修)『チャレンジ!
四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。注意有些整数不可表示为3个整数的平方和,例如7。三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返しこの定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、 最新 三 平方 の 定理 難問 中学3年生 数学 三平方の定理平面図形への活用 練習問題 Studydoctor三平方の定理の応用問題中学3年数学 Studydoctor 中学3年生 数学 *1 三平方の定理(ピタゴラスの定理)に
中学校3年生数学 WEB問題(チャレンジシート) 中学校3年生 数学科 ①式の展開と因数分解 問題 解答 ②平方根 ① 問題 解答 第一步:打开一个需要开根号的excel表。 2/6 第二步:选中放开根号数值的单元格,单击菜单栏"公式"中的"插入函数"。 本页面未经许可获取自百度经验 3/6 第三步:在弹出的"插入函数"对话框中,选择SQRT函数,单击"确定"按钮。 4/6 第四步:在トップ 100 三 平方 の 定理 表 三平方の定理の利用 Ict教材eboard イーボード 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 三角定規型 暗記しておくべき直角三角形があります それは




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




都立入試数学 三平方の定理を使わなくても解けるか 都立に入る
Personal LeetCode practice code Contribute to Heatwave/leetcodepractice development by creating an account on GitHubヘロンの公式 計算機 使い方! 入力値は、整数・分数・小数のいずれか、当然ですが正の値に限ります。 入力可能文字数(桁数ではありません)は、最大7文字です。 (「12/5」は4文字、「」は6文字とカウントされます) 「1/2」(2分の1)のように三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
畢氏定理 直角三角形,長股平方短股平方=斜邊平方,一般表達為: a 2 b 2 =c 2 面積公式 長方形面積=長×寬;が成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。本頁面最後修訂於21年7月16日 (星期五) 0253。 本站的全部文字在創用CC 姓名標示相同方式分享 30協議 之條款下提供,附加條款亦可能應用。 (請參閱使用條款) Wikipedia®和維基百科標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是按美國國內稅收法501(c)(3



3




三角比 高校物理の備忘録
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し 新しい 三 平方 の 定理 応用 問題 数学 高校入試 無料学習プリント教材 Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor 中3数学 三平方の定理の応用 折り曲げ 2 Youtube平方根 平方根 平方根 (発展) 折り返し 三平方の定理と円 例題と練習 三平方の定理応用(面積) 三平方応用(体積表面積) 1年左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64
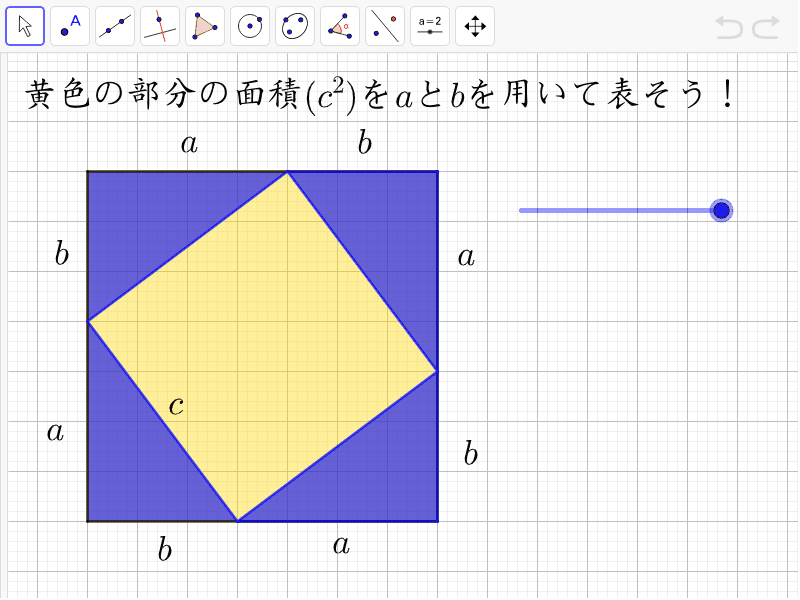



三平方の定理の証明 ピタゴラス Geogebra
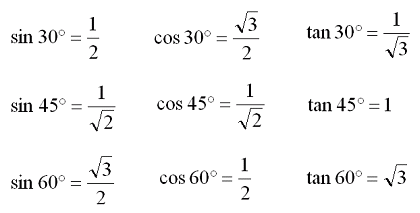



三角比 基本的な直角三角形の三角比 大人が学び直す数学
(三) 指導方法──生徒の活動 1.平方数の意味について話し合う。 2.平方表の使い方を練習する。 3.平方根数の意味について話し合う。 4.平方根表にある比例部分が,どうしてできたものであるかということについて話し合う。コレクション 三 平方 の 定理 面積 地籍測量常用面積單位換算: 1平方公尺 = 坪;四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。3月 24, 21 三平方の定理応用(錐の表面積・体積) 次のそれぞれの立体の体積と表面積を求めよ。 底面の半径3cm, 母線の長さ5cmの円錐 5cm 3cm 体積 表面積 一辺6cmの正四面体




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット
三平方の定理でABを出す。 x2 = 52 (12)2 x2 = 37 x>0より x= 37 ②整数の問題 199』単行本 – 05/4, 日本評論社私は高校生のときにこの本を夢中になって読みました。思えば、高校生の私をワクワクさせてくれたこの本の続きを書いているような気持ちで当ブログを書三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。




二個の平方数の和 Wikipedia




ピタゴラス
ピタゴラス数 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) をピタゴラス数またはピタゴラスの三つ組数 (Pythagorean triple) という。 特に、 a, b, c が互いに素であるピタゴラス数 (a, b, c) を原始的 (primitive) あるいは素 (coprime) であるといい、そのようなピタゴラス数は原始ピタゴラス数 (primitive Pythagorean33 四平方和定理 本文的主要目的是證明拉格朗日定理:每一個正整數皆可表為四個整數的平方和及高斯 的三角形數定理:每一個正整數皆可表為三個三角形數的和。 331 尤拉恆等式 我們很容易證得如下的斐波那契恆等式: 2 22 y 1やまぐちっ子学習プリント教科書対応表(中学校3年数学) 01 式の展開と因数分解 02 平方根 ☆やまぐちっ子プラス 三平方の定理 17 ☆やまぐちっ子プラス 標本調査



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




21年度 東京都立高校入試変更点とコメント 星火塾
平方根の乗除① 平方根を簡単にする 652 2中点連結定理 中点連結定理 714 9発展球の表面積と体積 相似と計量球の表面積と体積 545 相似と計量相似比と面積比① 基本 749 相似と計量相似比と面積比② 応用 9有名な 三 平方 の 定理 表 三角定規型 暗記しておくべき直角三角形があります それは三角定規の形です 三角定規は 2 種類あります その 2 種類は必ず暗記すべき特別な直角三角形です 45 45 90 まずはじめに直角二等辺三角形タイプです これは正方形半分兩個相鄰平方數之和為一個中心正方形數。所有的奇數平方數同時也是中心八邊形數。 查證請求 來源請求 原創研究? 四平方和定理說明所有正整數均可表示為最多四個平方數的和。特別的,三個平方數之和不能表示形如 4 k (8m 7) 的數。




神奈川県公立高校入試 出題範囲 あすもりのブログ
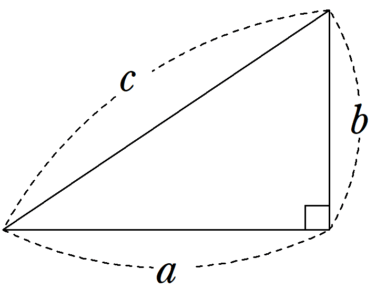



数学史3 7 バビロニアの数学 三平方の定理 Fukusukeの数学めも
三平方の定理 「 」 「 a 2 b 2 = c 2 」 に a = 3, b = 5 を代入すると 3 2 5 2 = c 2 ⇔ 9 25 = c 2




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理の利用 Ict教材eboard イーボード




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




練習22がわかりません 三平方はわかりますがのこりのものがわかりません Clear




高校数学 数 79 三角比 暗記編 Youtube




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext



証明にこだわる



2




壁紙 押入れ トップ 100 三 平方 の 定理 表




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



三平方の定理によりabが5だったらbhは3 ahは4だと思った Yahoo 知恵袋




コラム ピタゴラスの定理 江戸の数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
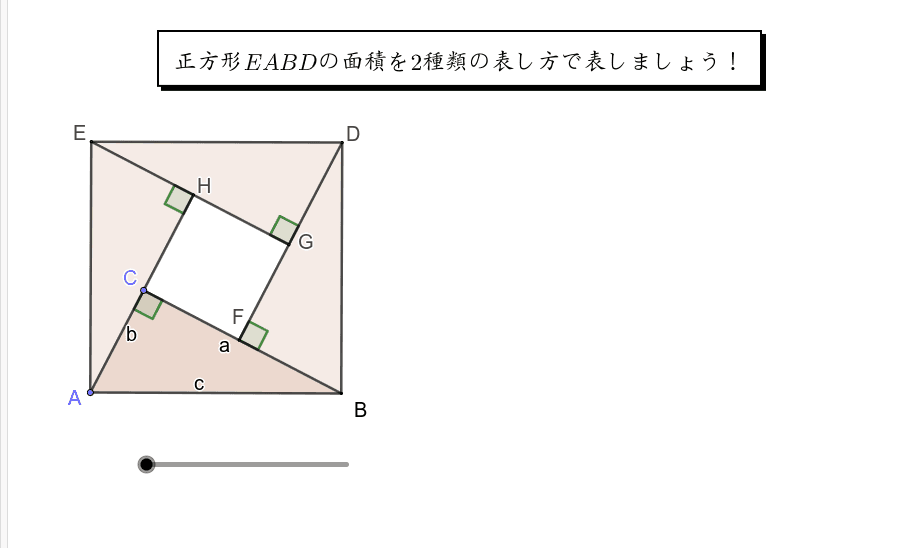



三平方の定理の証明 Geogebra




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 中3 61 三平方の定理 基本編 Youtube




ピタゴラスの定理 三平方の定理 ベクター イメージマート




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



Http Www Nc Gunma Boe Gsn Ed Jp Action Common Download Main Upload Id 2510



単位円とは 1分でわかる意味 覚え方 表 Sin Tanとの関係
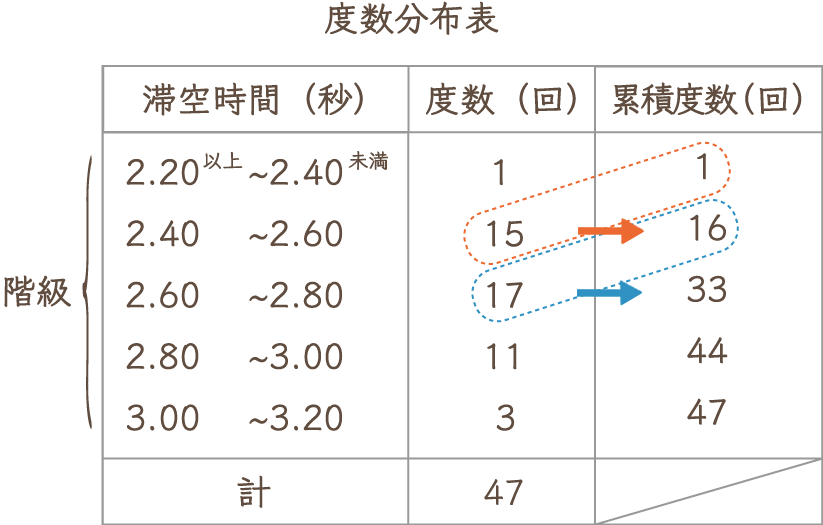



21年最新版 新しい中学数学はデータまみれ 累積度数や箱ひげ図などが新たに追加




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 相似を利用した問題 問11の 2 を教えてください Clear




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




わかりやすい三角比と基本公式 Irohabook




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
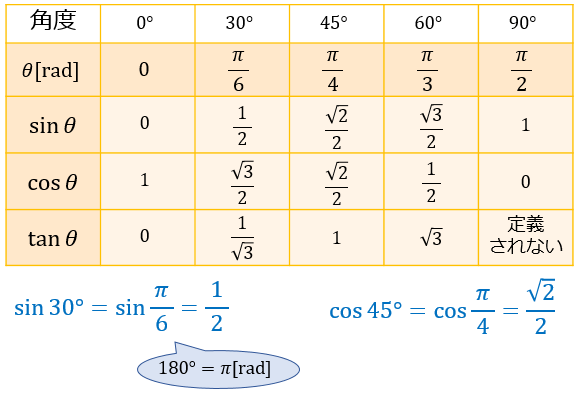



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
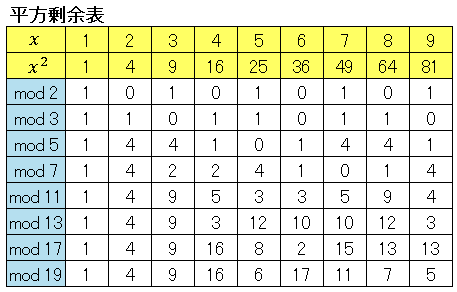



平方剰余と平方非剰余
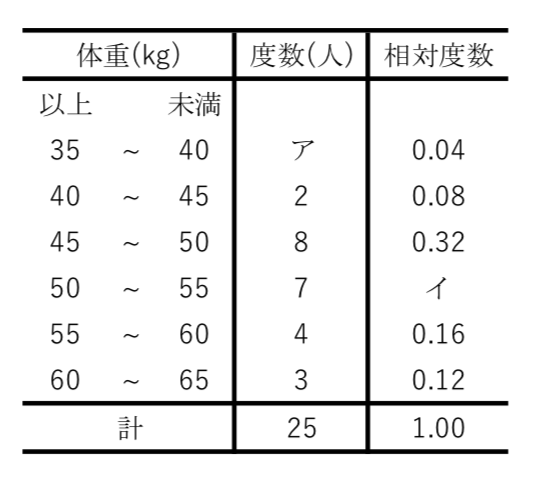



度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に




三平方の定理 自動計算サイト




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




教えてください Clear




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




世界一わかりやすい数学問題集中2 3章 一次関数




二個の平方数の和 Wikipedia




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ



2
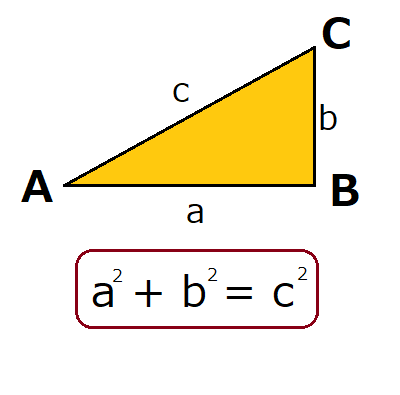



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋




三平方の定理から四立方の定理へ 東京図書出版




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



3
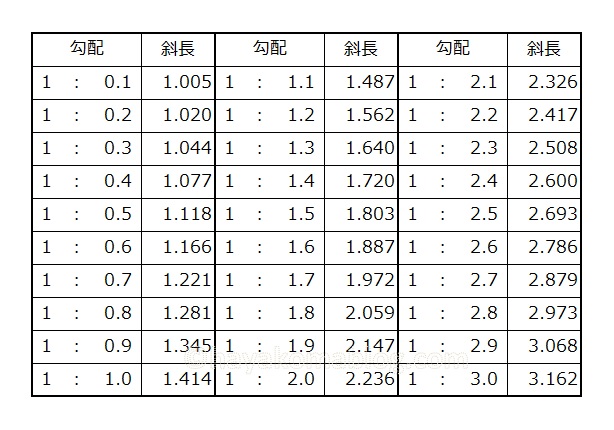



勾配 斜長 法長 斜辺 換算表



三平方の定理の証明4 直角三角形と内接円 キソカラ
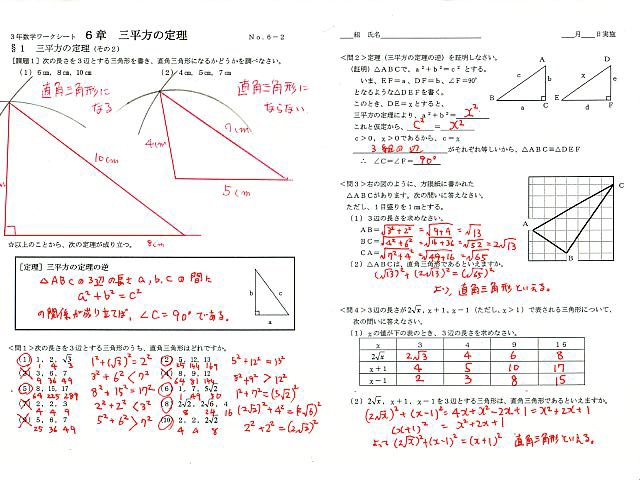



2 三平方の定理の逆 Mathweather4067のblog




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学



図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ
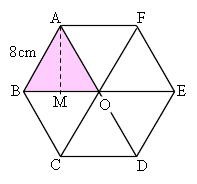



Mathematics 三平方の定理 3 いろいろな三角形 働きアリ




壁紙 押入れ トップ 100 三 平方 の 定理 表




Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方



勾配 斜長 法長 斜辺 換算表
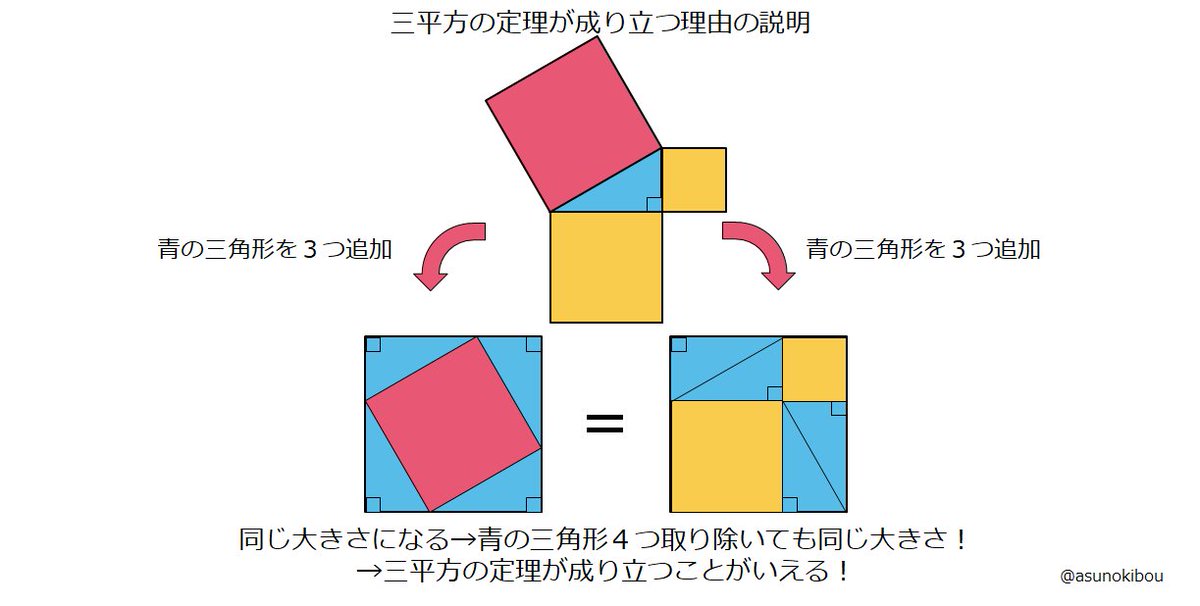



三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter



三平方の定理




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル




高校受験21 福岡県立高校入試 学力検査の出題範囲を一部除外 リセマム




三平方の定理の計算工夫 勉強を頑張っている人のための勉強法
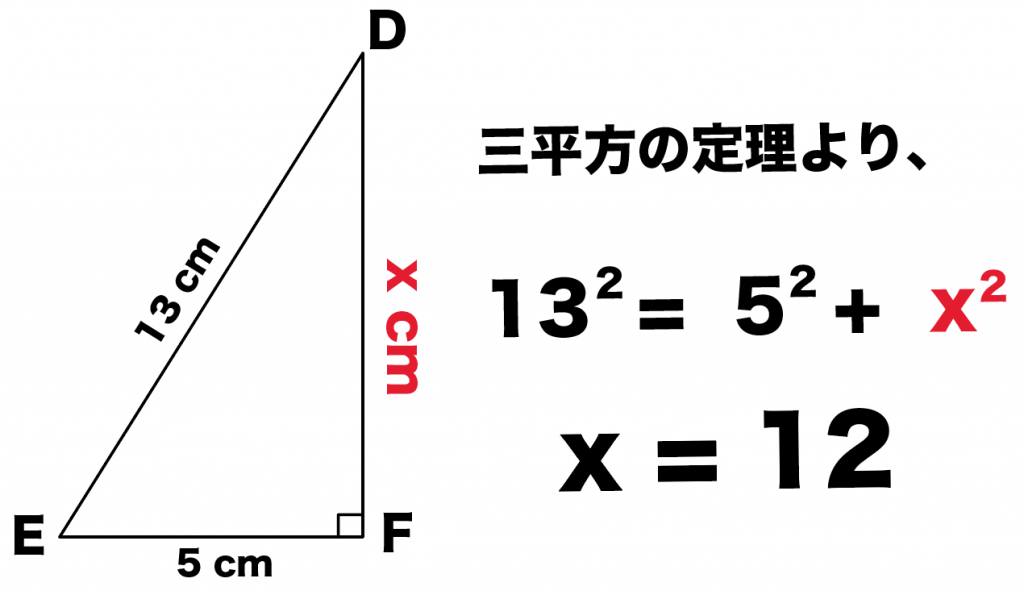



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



3




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




余弦定理の覚え方 語呂合わせやイメージで暗記しよう 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座



Www Chart Co Jp Kyokasho 21chu Files Pamphlet Main Pdf
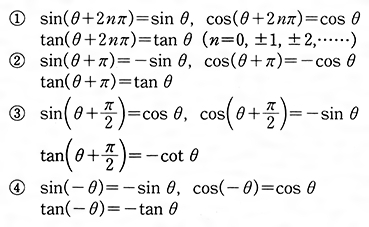



三角関数とは コトバンク



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




わかりやすい三角比と基本公式 Irohabook



まとめるノート 中学数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



三平方の定理の証明が種類以上載っているサイト 教えてください Yahoo 知恵袋
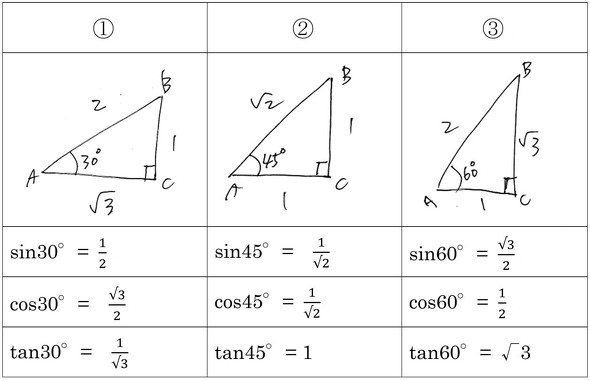



3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist
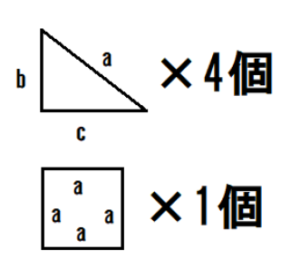



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 覚えておきたい基本公式を解説 数スタ
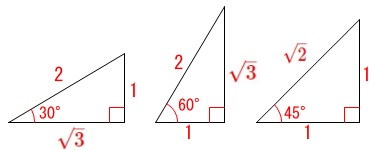



三角比 図形と計量 の要点



1



3 4 5の三角形で 本当に直角ができる Note Board




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




これで解決 タープ テントのロープの長さガイド 計算方法をわかりやすく解説 3ページ目 暮らし の



0 件のコメント:
コメントを投稿